Многоугольники

Начнем с определения многоугольников. Многоугольниками называют геометрические фигуры, образованные последовательным соединением нескольких точек, что приводит к образованию замкнутой ломаной линии. В результате такого соединения могут возникать различные многоугольники, такие как четырехугольники (см. рис. 1), пятиугольники (см. рис. 2) и шестиугольники (см. рис. 3).

Многоугольники классифицируются в зависимости от количества углов.

Прямоугольники

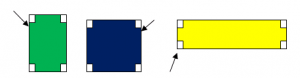
Теперь рассмотрим четырехугольники (см. рис. 4).

Каждый четырехугольник имеет 4 вершины, 4 стороны и 4 угла. Обратим особое внимание на углы этих фигур. Среди всех представленных многоугольников есть такие, у которых все углы являются прямыми (см. рис. 5). Эти четырехугольники называются прямоугольниками.

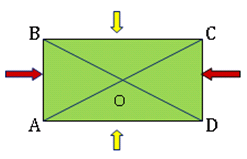
Теперь давайте подробнее рассмотрим прямоугольник (рис. 6). Известно, что противоположные стороны прямоугольника равны, например, AB = CD.

Если у прямоугольника все четыре стороны равны, то такая фигура называется квадратом (рис. 7).

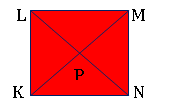
Отрезки AC и BD представляют собой диагонали прямоугольника, а отрезки EF и GH – диагонали квадрата. Важно отметить, что диагонали любого прямоугольника равны, то есть AC = BD, а для квадрата EF = GH. Это можно проверить с помощью циркуля: одну ножку циркуля ставим в точку A, а другую – в точку C (см. рис. 8).

Если ножки циркуля совпадают с точками B и D, это означает, что диагонали равны.

Точка пересечения диагоналей

Точка O – это точка пересечения диагоналей AC и BD (рис. 9). Эта точка делит диагонали на равные части, то есть отрезки AO, OC, BO и OD равны.

Поскольку квадрат является прямоугольником, точка O также делит диагонали на равные отрезки. Это можно проверить с помощью циркуля, установив одну ножку в точку O и вторую в точку E. Если ножки совпадают с точками F и G, значит, отрезки равны.

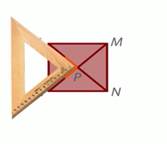
Кроме того, при пересечении диагоналей квадрата образуются четыре прямых угла. Это свойство можно проверить, приложив прямой угол прямоугольного треугольника к углу на чертеже.

Заключение

В ходе данного урока мы ознакомились с основными свойствами диагоналей квадрата и прямоугольника.

Свойства диагоналей квадрата

1. Диагонали квадрата равны
2. Все отрезки которые получаются при пересечении диагоналей квадрата равны
3. При пересечении диагоналей квадрата получается 4 прямых угла

Список рекомендованной литературы

1. Дмитриева О. И. Поурочные разработки по математике: 4 класс. – 3-е изд., перераб. и доп. – М.: ВАКО, 2012.
2. Моро М. И. Математика. 4 класс. Учебник в 2 частях. – М.: Просвещение, 2011.
3. Узорова О. В. Полный курс математики: все типы заданий, все виды задач, примеров, уравнений, неравенств, все контрольные работы, все виды тестов: 4 кл. – М.: Астрель, 2009.

Рекомендованные ссылки на ресурсы сети Интернет

• Интернет-портал «nsportal.ru»
• Интернет-портал «kopilkaurokov.ru»

Домашнее задание

1. Используя свойства диагоналей квадрата, нарисуйте квадрат, длина диагонали которого составляет 6 см.
2. Нарисуйте квадрат со стороной 5 см. Проведите диагонали и еще раз проверьте их три основных свойства.