Связь между умножением и делением. Периметр квадрата
Связь между сложением и вычитанием
Мы уже изучили, что операции сложения и вычитания имеют тесную взаимосвязь. Если из суммы вычесть первое слагаемое, то на выходе мы получим второе слагаемое. В свою очередь, если из суммы убрать второе слагаемое, то останется первое слагаемое. Это можно проиллюстрировать на примере (рис. 1).
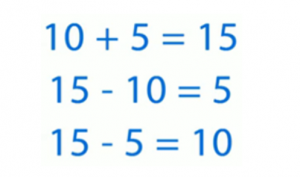
Рис. 1. Взаимосвязь сложения и вычитания
Взаимосвязь умножения и деления
Теперь давайте рассмотрим, как связаны действия умножения и деления. Начнем с составления выражения для умножения и попытаемся найти его результат. Для наглядности воспользуемся иллюстрацией.
4 ∙ 2 = …
Представим это в виде графического изображения (рис. 2).
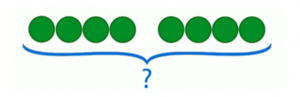
Рис. 2. Умножение 4 на 2
Когда мы говорим «4 умножить на 2», это означает, что мы повторяем 4 круга дважды. Каков же итог?
4 ∙ 2 = 8
Теперь давайте сформулируем выражение для деления, опираясь на данное равенство.
Рассмотрим равенство:
4 ∙ 2 = 8
Наша задача — выяснить, как умножение связано с делением.
Попробуем разделить полученное произведение на первый множитель.
8 : 4 = …
Это означает, что число 8 нужно распределить на 4 группы. Сколько кругов окажется в каждой группе?
Ответ: 2 круга (рис. 3).

Рис. 3. Деление числа 8 на 4 группы
Это значит, что 8 : 4 = 2.
Продолжим наше наблюдение. Составим из равенства 4 ∙ 2 = 8 еще одно выражение на деление.
8 : 2 = …
Это значит, что теперь число 8 нужно разделить на две одинаковые части (рис. 4).

Рис. 4. Деление числа 8 на две равные части
В каждой из этих частей содержится по 4 круга. Это означает, что:
8 : 2 = 4
Обратите внимание на следующие равенства:
4 ∙ 2 = 8
8 : 4 = 2
8 : 2 = 4
Если мы разделим произведение на первый множитель, то получим второй множитель. И наоборот, разделив произведение на второй множитель, мы получим первый. Это подтверждает, что умножение и деление взаимосвязаны.
Теперь давайте применим наши знания о связи между умножением и делением для решения новой задачи.
Периметр квадрата
Обратите внимание на рисунок (рис. 5).

Рис. 5. Квадрат
На нем изображена геометрическая фигура – квадрат. Давайте найдем периметр квадрата.
Что такое квадрат?
Квадрат – это прямоугольник, у которого все стороны равны. А если квадрат – это тоже прямоугольник, подходит ли формула для нахождения периметра прямоугольника
(a + b) ∙ 2 для нахождения периметра квадрата?
Давайте это выясним. Сначала найдем сумму длин сторон квадрата методом сложения.
Длина стороны квадрата ABCD – 5 см (рис. 6).
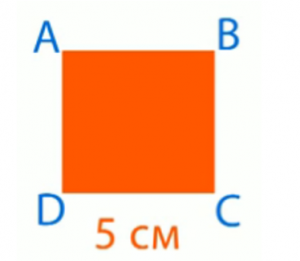
Рис. 6. Длина стороны квадрата ABCD
Чтобы вычислить периметр квадрата, необходимо сложить длины всех его сторон. Это можно представить следующим образом:
5 + 5 + 5 + 5
Вы могли заметить, что мы складываем одинаковые значения. Это позволяет нам заменить операцию сложения на умножение. Давайте сделаем это.
Каждое слагаемое равно 5, и таких слагаемых у нас 4.
5 + 5 + 5 + 5
Таким образом, мы можем преобразовать выражение для нахождения суммы в выражение для нахождения произведения:
5 + 5 + 5 + 5 = 5 ∙ 4
Это означает, что для вычисления суммы длин сторон квадрата нужно умножить длину одной стороны на количество сторон.
Формула для вычисления периметра квадрата
Теперь давайте сформулируем правило для нахождения периметра квадрата.
Чтобы найти периметр квадрата, необходимо умножить длину его стороны, независимо от ее величины, на 4 (рис. 7).

Рис. 7. Формула для вычисления периметра квадрата
Что делать, если у нас уже есть значение периметра квадрата?
Теперь, когда мы знаем формулу для вычисления периметра квадрата, мы можем использовать её не только для нахождения периметра, но и для определения длины его стороны.
Согласно формуле a⋅4a⋅4, чтобы найти периметр квадрата, мы умножаем длину стороны на 4 — количество сторон. Например, если длина стороны квадрата составляет 5 см, то:
5⋅4=20 см5⋅4=20см
А что если известен периметр квадрата, и нам нужно определить длину его стороны?
Периметр квадрата представляет собой сумму длин его сторон. Поскольку у квадрата четыре стороны, для нахождения длины одной стороны нужно разделить периметр на известный множитель. В нашем случае этот множитель — 4. Если периметр равен 20 см, то:
20:4=5 см20:4=5см
Теперь вспомним, как вычислять периметр другой геометрической фигуры, а именно, прямоугольника.
Периметр прямоугольника
Чтобы вычислить периметр фигуры, необходимо найти сумму длин всех её сторон. Прямоугольник — это четырехугольник, в котором противоположные стороны равны. В прямоугольнике ABCD стороны AB и DC равны, а также AD и BC.
AB=DCAB=DC
AD=BCAD=BC
Чтобы вычислить периметр прямоугольника ABCD, сначала определим полупериметр, который является суммой двух соседних сторон (AB + BC). Поскольку у нас есть по две равные стороны, полупериметр нужно умножить на 2. Таким образом, формула для нахождения периметра прямоугольника ABCD будет выглядеть следующим образом (рис. 8):
(AB+BC)⋅2(AB+BC)⋅2

Рис. 8. Формула для нахождения периметра прямоугольника
Для того чтобы найти периметр или сумму всех сторон, нужно сначала найти полупериметр. Полупериметр – это сумма одной длины и одной ширины фигуры. Затем умножаем полупериметр на 2, потому что стороны прямоугольника попарно равны (рис. 9).
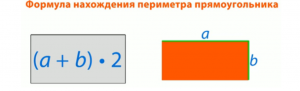
Рис. 9. Формула для вычисления периметра прямоугольника
Итоги урока
В ходе данного урока мы изучили, как с помощью взаимосвязи между умножением и делением находить периметр квадрата и определять длину его стороны.
Список литературы
- Александрова Э. И. Математика. 2 класс. – Москва: Дрофа, 2004.
- Башмаков М. И., Нефёдова М. Г. Математика. 2 класс. – Москва: Астрель, 2006.
- Дорофеев Г. В., Миракова Т. И. Математика. 2 класс. – Москва: Просвещение, 2012.
Дополнительные рекомендованные ресурсы в интернете
- Интернет-портал «math-prosto.ru» (Источник)
- Интернет-портал «urok.1sept.ru» (Источник)
Домашнее задание
Теперь, когда мы усвоили материал, попробуйте самостоятельно решить несколько задач на нахождение периметра различных фигур, используя изученные формулы.
1. Найдите периметры фигур:
а) 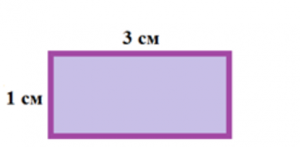
б) 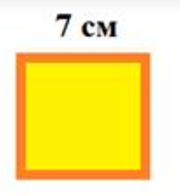
в) 
2. Решите выражения:
а) 2 ∙ 6 б) 16 : 2 в) 36 : 4
3. Сравните выражения:
а) 14 : 2 и 14 : 7 б) 12 : 4 и 12 : 3 в) 18 : 3 и 12 : 2
Оцените урок:





