Задания про лягушек на построение равенства

На этом уроке вы познакомитесь с математическими понятиями «равенство» и «неравенство».

Пожалуйста, попробуйте ответить на вопрос:

На стене есть ванна,

В каждой ванне ровно по 1 лягушке.

если бы ванн было пять,

Сколько среди них будет лягушек (рис. 1). 1)?

Рис. 1

В стихотворении говорится, что кадушек было 5, в каждой кадушке по 1 лягушке, никто не остался без пары, значит число лягушек равно числу кадушек.

Обозначим кадушки буквой К, а лягушек – буквой Л.

Запишем равенство: К = Л (рис. 2).

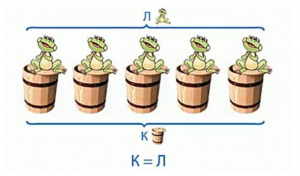
Рис. 2

Способ сравнения групп фигур с помощью составления пар

Сравните по количеству две группы фигур. Фигур много, они разного размера, расположены без порядка (рис. 3).

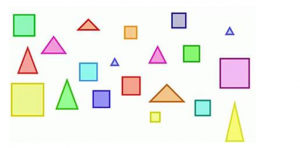
Рис. 3

Составим из этих фигур пары. Каждый квадрат соединим с треугольником (рис. 4).

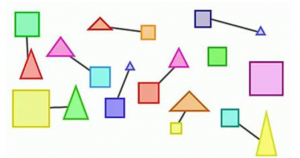
Рис. 4

Два квадрата остались без пары. Значит, количество квадратов не равно количеству треугольников. Обозначим квадраты буквой К, а треугольники – буквой Т.

Запишем неравенство: К ≠ Т (рис. 5).

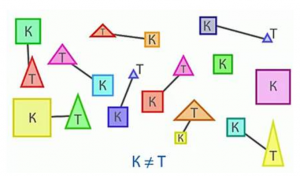
Рис. 5

Равенство

Вывод: Создав пару, вы можете сравнить количество элементов в 2 группах. Если все элементы имеют пары, то соответствующие числа равны, и в этом случае мы ставим знак равенства между цифрами или буквами. Эта запись называется эквивалентной (рис. 1). 6).

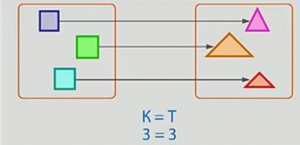
Рис. 6

Неравенство

Если пар недостаточно, то есть есть лишние элементы, то эти числа не равны. Поставьте знак неравенства между цифрами или буквами. Эта запись называется неравенством (рис. 1). 7).

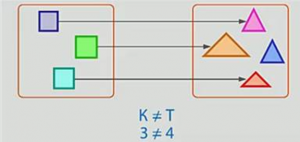
Рис. 7

Оставшиеся без пары элементы показывают, какое из двух чисел больше и на сколько (рис. 8).

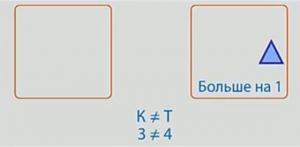
Рис. 8

Сравнение чисел с помощью числового луча

Способ сравнения групп фигур с помощью составления пар не всегда удобен и занимает много времени. Можно сравнивать числа с помощью числового луча (рис. 9).

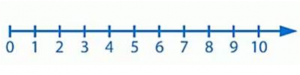
Рис. 9

Пример 1 при сравнении чисел с помощью числового луча

Используйте числовые лучи для сравнения этих чисел и присвойте им символ сравнения.

Пример 1

2  ⃞  5

Нам нужно сравнить числа 2 и 5. Давайте посмотрим на числовые лучи. Скажем, 2 в числе ближе к 0, чем 5 в числе, или 2 в луче числа находится левее, чем 5 в числе. Таким образом, 2 не равно 5. Это неравенство.

2 ≠ 5

Символ «π» (не равно) только исправляет неравенство в числах и не указывает, какое из них больше, а какое меньше.

Из 2 чисел на числовом луче меньшее находится слева, а большее — справа (рис. 1). 10).

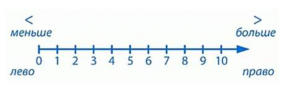
Рис. 10

Можно данное неравенство записать по-другому, используя знак меньше « < » или знак больше  « > »:

2 < 5

Пример 2 на сравнение чисел с помощью числового луча

Пример 2

7   ⃞  4

На числовом луче число 7 находится правее, чем число 4, следовательно:

7 ≠ 4 и 7 > 4

Пример 3 на сравнение чисел с помощью числового луча

Пример 3

9  ⃞  9

Числа 9 и 9 равны, поэтому ставим знак =, это равенство:

9 = 9

Задание на сравнение количества точек и числа

Сравните количество точек и число и поставьте соответствующий знак (рис. 11).

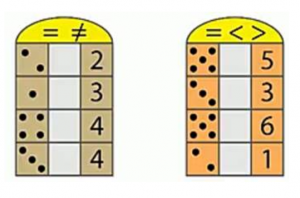
Рис. 11

На первом рисунке нам необходимо поставить знак = или ≠.

Сравниваем две точки и число 2, ставим между ними знак =. Это равенство.

Сравниваем одну точку и число 3, на числовом луче число 1 находится левее, чем число 3, ставим знак ≠.

Сравниваем четыре точки и 4. Между ними ставим знак =. Это равенство.

Сравниваем три точки и число 4. Три точки – это число 3. На числовом луче оно левее, ставим знак ≠. Это неравенство (рис. 12).

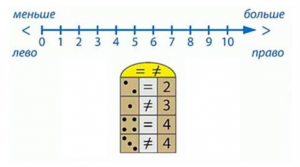
Рис. 12

На втором рисунке между точками и числами надо поставить знаки =, <, >.

Сравним пять точек и число 5. Между ними ставим знак =. Это равенство.

Сравним три точки и число 3. Здесь тоже можно поставить знак =.

Сравним пять точек и число 6. На числовом луче число 5 левее, чем число 6. Ставим знак <. Это неравенство.

Сравним две точки и единицу, число 2 правее на числовом луче, чем число 1. Ставим знак >. Это неравенство (рис. 13).

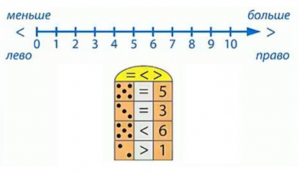
Рис. 13

Задача состоит в том, чтобы найти числа для уравнений и неравенств

Вставьте число в окно так, чтобы полученные в результате равенства и неравенства были истинными.

1. ⃞ < 7

Это неравенство. Давайте посмотрим на числовые лучи. Если вы ищете число, меньшее числа 7, оно должно быть слева от числа 7 на числовом луче (рис. 1). 14).

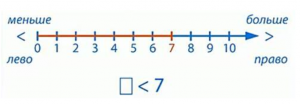
Рис. 14

В окошко можно вставить несколько чисел. Сюда подходят числа 0, 1, 2, 3, 4, 5, 6. Любое из них можно подставить в окошко и получить несколько верных неравенства. Например, 5 < 7 или 2 < 7.

2. 5 > ⃞

На числовом луче найдём числа, которые будут меньше 5 (рис. 15).

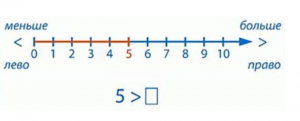
Рисунок 2.1.1. 15

Это числа 4, 3, 2, 1, 0. Таким образом, вы можете вставить любое из этих чисел в окно и получить несколько правильных неравенств. Например, 5>4, 5>3.

3. 8 = ⃞

Вы можете поместить в него только 1 цифру 8.

8 = 8.

На этом уроке мы познакомились с математическими понятиями «равенство» и «неравенство», научились правильно размещать символы сравнения, попрактиковались в сравнении групп чисел с помощью пар и сравнении чисел с помощью числовых лучей.Это поможет дальнейшему изучению математики.

Список литературы

Александрова Л.А.,Мордкович А.Г.Математика. 1 класс. -М.: Мнемозина,2012.
Башмаков М.И.,Нефедова М.Г.Математика. 1 класс. — М.: Астрель, 2012.
Беденко М.В.Математика. 1 класс. -М7: Русский язык, 2012.

Дополнительные рекомендуемые ссылки на интернет-ресурсы

Интернет-портал»igraem.pro «(Источник)

Домашнее задание

1. Какие знаки сравнения вы знаете, в каких случаях они используются? Запишите знаки сравнения чисел.

2. Сравните количество предметов на рисунке и поставьте знак «<», «>» или «=».

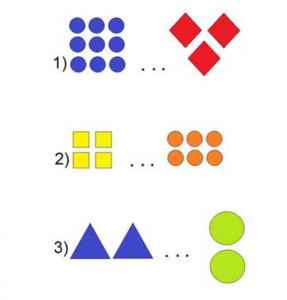
3. Сравни числа, поставив знак «<», «>» или «=».