На этом уроке мы познакомимся с основным свойством дробей, разберемся, что такое эквивалентные дроби, и научимся сокращать дроби. Также мы выясним, как определить, является ли дробь сократимой, и когда стоит использовать сокращение, а когда нет.

Если вам будет сложно понять материал, вы можете обратиться к уроку «Часть 2. Дроби. Рациональные числа».

Основное свойство дроби

Представьте ситуацию: за столом сидят 3 человека и у них 5 яблок. Если эти яблоки поделить между всеми, то каждый получит по 5335​ яблока.

Теперь представьте, что за соседним столом также 3 человека и тоже 5 яблок. Каждый из них также получит по 5335​ яблока.

Таким образом, у нас есть 10 яблок и 6 человек, и каждый получит по 106610​ яблока, что равно 5335​. Эти дроби эквивалентны.

Можно увеличить количество людей и яблок вдвое, и результат останется тем же.

В математике это выражается так: если числитель и знаменатель дроби умножить или разделить на одно и то же число (кроме нуля), то новая дробь будет равна исходной. Это свойство называется «основным свойством дроби».

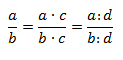
Примеры эквивалентных дробей

1. Путь от города до деревни – 7 км.

Мы идем по дороге и определяем пройденный путь по километровым столбикам. Пройдя три столбика, три километра, мы понимаем, что прошли 3/7 пути.

Но если мы не видим столбиков (может, их не установили), можно путь считать по электрическим столбам вдоль дороги. Их 20 штук на каждый километр. То есть всего 140 на всем пути. Три километра – 3 * 20 = 60 столбов. То есть мы прошли 60 из 140 столбов, 60/140.

2. Дробь на координатной плоскости можно отмечать точкой. Чтобы изобразить дробь 3/4 отметим точку с координатой 3 по оси Y и 4 по оси X. Проведем прямую из начала координат через нашу точку.

На этой же прямой будет лежать и точка, соответствующая дроби 6/8.

Они являются эквивалентными:  (см. Рис. 1)

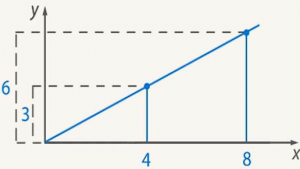
Рис. 1. Иллюстрация к примеру

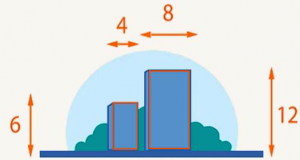
3. На рисунке 2 два дома. Первый – высотой 6 метров и шириной 4, а второй – высотой 12 метров и шириной 8. Размеры разные, но дома по форме похожи. У них одинаковые пропорции, одинаковое отношение высоты к ширине.

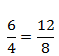
Сокращение дроби

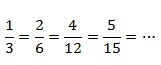
Дробь 4/12 можно было получить из 1/3 умножением числителя и знаменателя на 4:

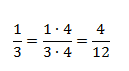
или из 2/6 умножением на 2:

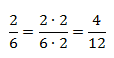
Но точно так же можно и вернуться назад.

У дроби 4/12 можно числитель и знаменатель разделить на 2, получить 2/6:

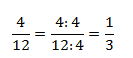
Или числитель и знаменатель разделить на 4, получить 1/3:

Вот такой переход от одной дроби к другой с помощью деления числителя и знаменателя на одно и то же число называется сокращением дроби.

У дроби 400/500 можно разделить числитель и знаменатель на 100. Получим 4/5.

Это эквивалентная запись, но она короче. Мы сократили запись. Сократили дробь:

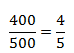
Сократимые и несократимые дроби

Посмотрим еще раз на цепочку эквивалентных дробей.

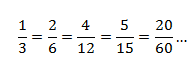
Дробь 4/12 можно сократить на 2 и получить 2/6 или сократить на 4 и получить 1/6.

Дробь 5/15 нам не получится сократить до 4/12 или 2/6, зато легко сократить на 5 и получить 1/6.

Только одну дробь из представленных мы не можем сократить: 1/6.

Такая дробь называется несократимой. Ее нельзя сократить.

Остальные сократимые. Их можно сократить.

Рассмотрим дробь .

Чтобы понять, можно ли ее сократить, нужно узнать, существует ли число, на которое делится и числитель, и знаменатель, есть ли общий делитель.

42 делится на 2, но 273 на 2 не делится.

42 делится на 3 (сумма цифр 6 делится на 3), и 273 делится на три (сумма цифр 12).

Значит, мы можем поделить числитель и знаменатель на 3, сократить дробь на 3.

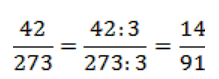
Можно ли сократить полученную дробь дальше?

14 делится на 2 и на 7.

91 не делится на 2, но на 7 делится.

Значит, дробь можно сократить на 7.

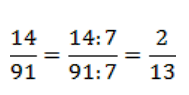
Для чисел 2 и 13 нам уже не найти общего делителя.

Дробь 2/13 несократима.

Не всегда легко, глядя на дробь, понять, можно ее сократить или нет.

Что нам может помочь в этом?

Чтобы сократить дробь, нужно найти общий делитель для числителя и знаменателя.

Но делители числа и его множители – это одно и то же.

10 = 2 * 5

2 и 5 – это множители, но на них можно разделить. Поэтому они же и делители.

То есть разложение на множители – это и разложение на делители.

Вернемся к нашему примеру.

Если бы числитель и знаменатель были разложены на множители, мы бы сразу поняли, как сократить дробь.

Общие множители (делители) – 3 и 7. На них и сокращаем.

Задача

В школе 4 первых класса, и в каждом учится 27 учеников.

Есть 12 коробок мандаринов, в каждой по 45 штук. Сколько каждому первокласснику достанется мандаринов, если их поделить поровну?

Понятно, что надо количество мандаринов разделить на количество первоклассников.

Найдем и то и другое.

4 * 27 = 108 первоклассников.

12 * 45 = 540 мандаринов.

Осталось разделить.

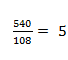 мандаринов на первоклассника.

Но можно было и упростить себе задачу, ведь у нас уже было разложение на множители:

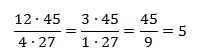
Не будем сразу считать, сколько мандаринов и сколько учеников. Сначала сократим нашу дробь. 12 и 4 делятся на 4. 3 и 27 делятся на 3.

Это решение оказалось проще.

Задание 1

Сократите следующие дроби самостоятельно:

1. 24363624​
2. 45606045​
3. 18545418​

Проверка

1. 2436=233624​=32​
2. 4560=346045​=43​
3. 1854=135418​=31​

Задача 2

Докажите, что дробь несократима:

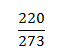
Проверка:

разложим на простые множители числитель и знаменатель:

Общих множителей (общих делителей) нет. Значит, сократить невозможно. Дробь несократима.

Такие числа, как 220 и 273, не имеющие общих делителей, кроме 1, мы называем взаимно простыми.

То есть можно сказать про несократимую дробь следующее: дробь несократима, если ее числитель и знаменатель – взаимно простые числа.

Заключение

Сокращение дроби означает деление числителя и знаменателя на одно и то же число (не равное нулю), в результате чего мы получаем эквивалентную дробь с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно проверить, на что делятся числитель и знаменатель, и найти общий делитель.

Всегда ли нужно сокращать?

Иногда удобнее оставить дробь в исходном виде. Например, фраза «Цена выросла на 20 %» может быть представлена как 2010010020​. Сокращение возможно, но в данном случае удобнее оставить в процентах.

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. «Математика 6». – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. «Математика 6 класс». – Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. «За страницами учебника математики». – М.: Просвещение, 1989.

Дополнительные ресурсы

• Интернет-портал «school-assistant.ru»
• Интернет-портал «matematika-na.ru»
• Интернет-портал «urok.1sept.ru»

Домашнее задание

1. Сократите заданные дроби. Если дробь десятичная, представьте ее в виде обыкновенной дроби.
2. Решите задачу: на уроке физкультуры ученики 2 класса прыгали с места. Вася прыгнул на расстояние $x$ метров, а Коля – на расстояние $y$ метров. Чей прыжок длиннее и на сколько сантиметров?
3. Сравните дроби: 3443​ и 6886​; 510105​ и 1221​; 912129​ и 3443​; 816168​ и 1221​.