Как выполнять деление обыкновенных дробей? Как разделить смешанные числа? Как найти частное при делении обыкновенной дроби на натуральное число? Этот урок будет посвящен подробному разбору этих вопросов. Новое правило будет проиллюстрировано примерами.

Во второй части урока мы сосредоточимся на задачах, связанных с составлением уравнений. Представленные рассуждения помогут продолжить развитие навыка решения задач данного типа.

Введение в понятие взаимно обратных чисел

Два числа называются взаимно обратными, если их произведение равно 1.

Например, обратное для числа 2 – это 1/2, т. к. их произведение равно 1. Для числа 4 обратное 1/4. Для числа 1 обратное 1.

Для числа 2/3 обратное 3/2, т. к. произведение этих дробей равно 6/6 = 1. (Аналогично, если сразу сократить 2 и 3 в числителе и знаменателе.)

Таким образом, обратное число для дроби – перевёрнутая дробь, т. е. для дроби a/b обратной будет b/a. Это же правило работает и для целых чисел, если записать, например, число 2 как 2/1.

Правило деления обыкновенных дробей

Зачем нужна операция деления обыкновенных дробей? Рассмотрим пример.

Задача 1. Пусть дан прямоугольник и площадь этого прямоугольника равна 5/8 м². Длина прямоугольника равна 3/8м. Чему равна ширина прямоугольника?

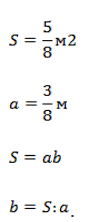
Чтобы найти ширину, нам нужно 5/8 разделить на 3/8. Но мы этого не умеем делать, поэтому запишем . Теперь умножим левую и правую часть на число, обратное 3/8, т. е. 8/3. Тогда получим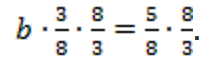

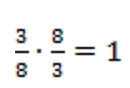 (т. к. числа взаимно обратные)

Тогда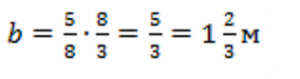

Теперь сформулируем правило.

Решение примеров

Решение примеров

Пример 1. Разделить 1/2 на 3/4.

Решение

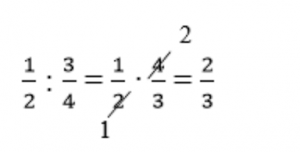
Пример 2. Разделить 5/7 на 6/7.

Решение:

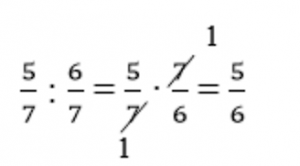
Пример 3. Разделить 1/3 на 4.

Решение: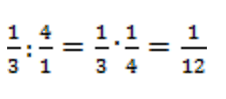

Решение примеров со смешанными числами

Для деления смешанных чисел нужно перевести число в неправильную дробь, а затем выполнить деление по алгоритму.

Пример 4. Разделить

Решение: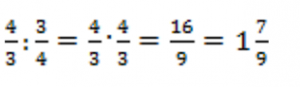

Пример 5. Разделить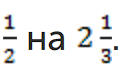

Решение: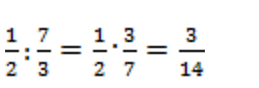

Пример 6. Разделить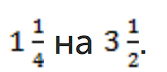

Решение:

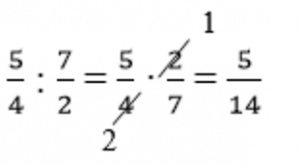
Задача 2. Машина проехала 70 км за 72 минуты. С какой скоростью шла машина на этом участке?

Запишем условие.

Дано:

S = 70 км

t = 72 мин

V = ?

Переведём время в часы.

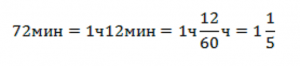
Чтобы найти скорость, нужно расстояние разделить на время, т. е.

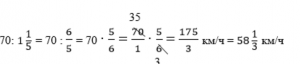
Ответ:

Заключение

В ходе нашего урока мы изучили процесс деления обыкновенных дробей, который можно свести к умножению. Правило деления гласит: чтобы разделить одну дробь на другую, необходимо умножить первую дробь на обратную второй дроби. Мы также выяснили, что этот алгоритм применим как для неправильных дробей (включая смешанные числа), так и для целых чисел.

Рекомендованная литература

1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика для 6 класса.
2. Мерзляк А. Г., Полонский В. В., Якир М. С. Математика для 6 класса.

Дополнительные онлайн-ресурсы

• Интернет-ресурс «school-assistant.ru» (Источник)
• Интернет-ресурс «math-prosto.ru» (Источник)

Домашнее задание

1. Найдите число, обратное данному числу: 

2. Выполните деление:

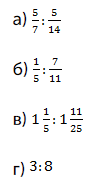
3. За 5/8 ч мотоциклист проехал  км. С какой скоростью ехал мотоциклист?