Дробное выражение

Что же такое дробь? Например, дробь 7/12 – это деление числа 7 на число 12, записанное с помощью дробной черты.

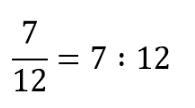
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.

Примеры дробных выражений:

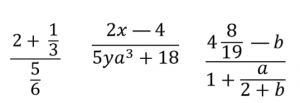
Дробь 7/12 также является дробным выражением.

Упрощение дробных выражений

У дробного выражения существуют эквивалентные, равные ему, выражения. Выбрать из всех эквивалентных выражений самое простое – значит упростить дробное выражение.

Пример 1.

Упростить дробное выражение:

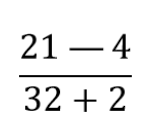
Решение:

Выполним вычитание в числители и сложение в знаменателе:

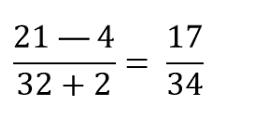
Разделим числитель и знаменатель на 17:

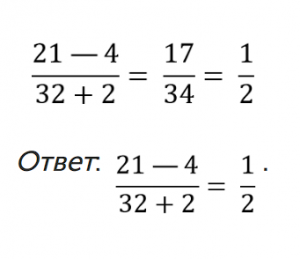
Задача 1

Упростите дробное выражение:

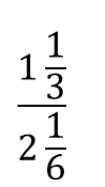
Решение:

В числителе и знаменателе – смешанные дроби. Чтобы разделить одну смешанную дробь на другую, нужно обе записать как неправильные.

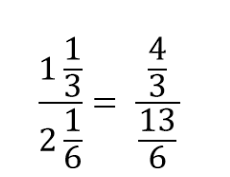
Получившееся дробное выражение эквивалентно произведению дробных выражений:

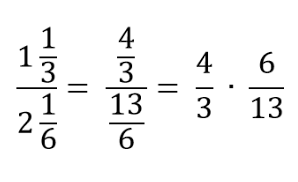
Сократим знаменатель первой дроби и числитель второй дроби на 3:

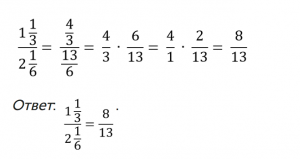
Задача 2

Сложите дробные выражения:

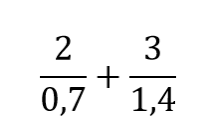
Решение:

1 способ

Приведём эти дробные выражения к одному знаменателю, для этого умножим числитель и знаменатель первой дроби на 2:

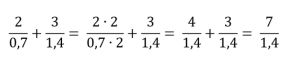
Чтобы избавиться от десятичной дроби в знаменателе, умножим числитель и знаменатель на 10:

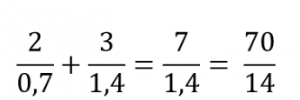
Сократим числитель и знаменатель на 7:

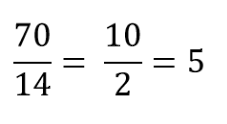
2 способ

Можно сразу избавиться от десятичных дробей в знаменателях, для этого умножим числитель и знаменатель каждой дроби на 10:

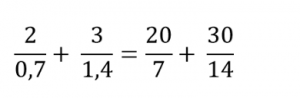
Далее приводим два дробных выражения к общему знаменателю:

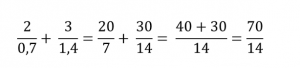
Сократим числитель и знаменатель на 7:

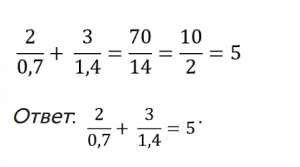
Задача 3

Упростите дробное выражение:

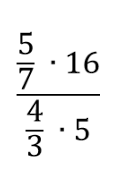
Решение:

Преобразуем числитель и знаменатель в обыкновенные дроби:

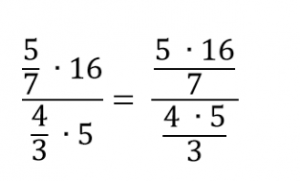
Запишем получившееся выражение с помощью знака деления:

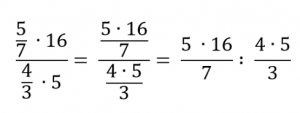
Чтобы разделить на дробь, нужно умножить на перевернутую дробь:

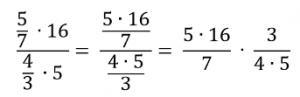
Числитель первой дроби и знаменатель второй можно сократить на 5 и на 4.

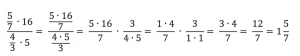
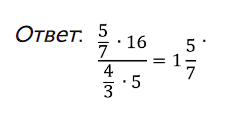
Задача 4

Упростите дробное выражение:

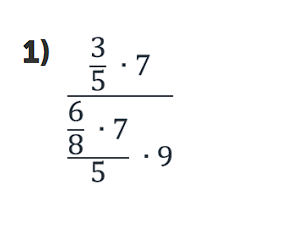
Решение:

Преобразуем числитель и знаменатель в обыкновенные дроби:

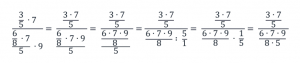
Запишем это дробное выражение с помощью знака деления, а далее заменим знак деления на знак умножения и перевернем вторую дробь:

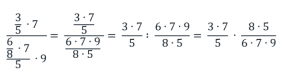
Сократим числитель первой дроби и знаменатель второй на 3 и 7, а числитель второй дроби и знаменатель первой – на 5:

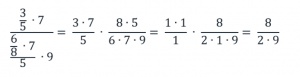
Сократим числитель и знаменатель на 2:

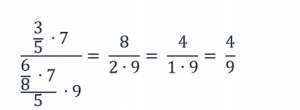
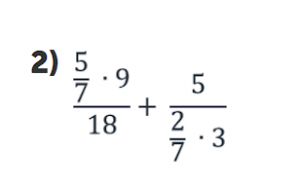
Решение:

Преобразуем числитель первого дробного выражения и знаменатель второго:

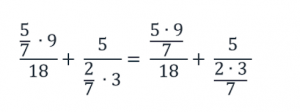
Распишем данные дробные выражения с помощью знака деления:

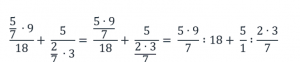
Заменим знаки деления на знаки умножения и перевернем соответствующие дроби:

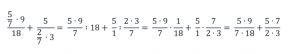
Первое дробное выражение сократим на 9:

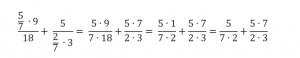
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:

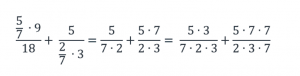
Вычислим числители обеих дробей и сложим эти дроби:

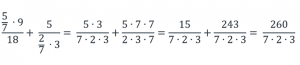
Сократим полученную дробь на 2:

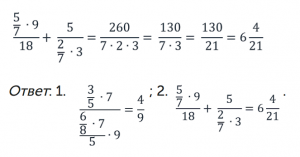
Преобразование «многоэтажных» дробей

Существует простой алгоритм, который позволяет за одно действие преобразовать «многоэтажную» дробь в обычную «двухэтажную».

Для этого нужно провести дробную черту после знака равенства и определить положение каждого элемента из «многоэтажной» дроби в новой дроби. Рассмотрим каждое число в исходной дроби.

• Если число встречается в знаменателе исходной дроби нечетное количество раз, то в новой дроби оно окажется в знаменателе.
• Если число встречается в знаменателе четное количество раз или вовсе отсутствует в знаменателе, то в новой дроби оно будет в числителе.

Теперь рассмотрим примеры для упрощения дробных выражений.

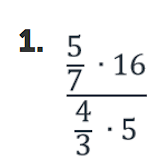
Рассмотрим каждое число данного дробного выражения:

Число 5 (в данном выражении две пятерки, их рассматриваем отдельно) находится в числителе дроби 5/7 и в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе дроби 5/7 и в числителе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;

число 16 находится в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 4 находится в числителе дроби 4/3 и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;

число 3 находится в знаменателе дроби 4/3 и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе четное число раз, следовательно, в новой дроби это число окажется в числителе;

число 5 находится в знаменателе всего дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе.

Запишем полученное дробное выражение:

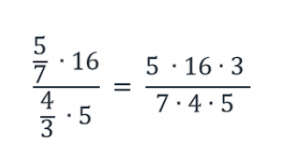
Сократим числитель и знаменатель на 5 и на 4:

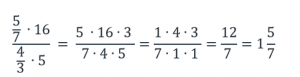
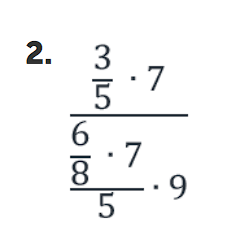
Рассмотрим каждое число данного дробного выражения:

Число 3 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 5 находится в знаменателе дроби 3/5, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 7 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 6 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 8 находится в знаменателе дроби 6/8 и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 5 находится в знаменателе всего дробного выражения и в знаменателе выражения 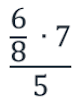, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 9 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

Запишем полученное дробное выражение:

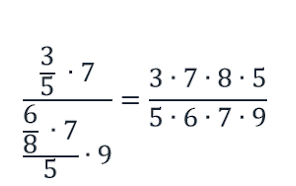
 Сократим числитель и знаменатель на 5, 7, 2 и 3:

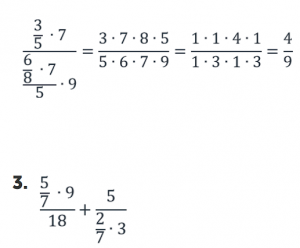
Рассмотрим числа в каждом дробном выражении:

а) выражение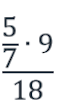

Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 7 находится в знаменателе дроби 5/7, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 9 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 18 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

б) выражение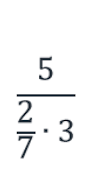

Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;

число 2 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;

число 7 находится в знаменателе дроби 2/7 и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;

число 3 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.

Запишем полученные дробные выражения:

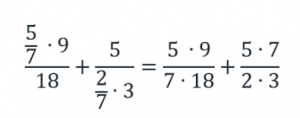
Сократим числитель и знаменатель первого выражения на 9:

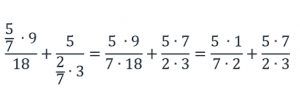
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:

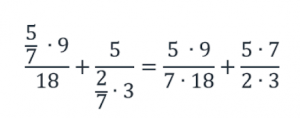
Вычислим числители обеих дробей и сложим эти дроби: 

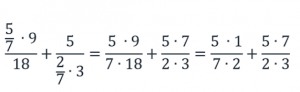
Сократим полученную дробь на 2:

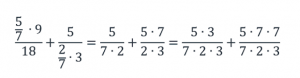
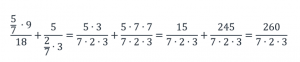
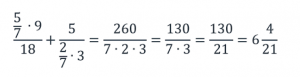
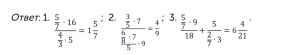
Задача 5 (дробные выражения с переменными)

Чтобы найти значение выражения с переменными, необходимо подставить в это выражение значения этих переменных. Но предварительно имеет смысл упростить выражение, если это возможно.

Найти значение выражения.

Решение:

Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:

Решение:

Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:

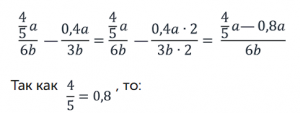
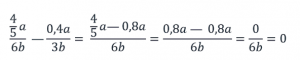
Мы получили ответ, даже не подставив значения переменных.

Ответ: 1) 1; 2) 0.