Координаты на прямой
На этом уроке мы поговорим о том, что такое координаты и координатная прямая. Научимся использовать координатную прямую для наглядного выполнения различных операций с числами.
Введение
Вот такие отметки на дороге (рис. 1) выполняют сразу три функции.
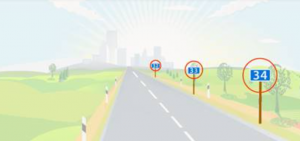
Рис. 1. Отметки на дороге
- Измерение расстояний. Мы знаем, на сколько мы удалились от города. Или от другой подобной отметки.
- Адрес, имя. Мы знаем, где находимся. По телефону легко передать числовой адрес нашего места.
- Направление. Глядя на эти отметки, легко понять, в какой стороне находится город – начало отсчета.
Где ещё числа помогают нам ориентироваться? В кинотеатре. В зрительном зале все ряды и все кресла пронумерованы. И на нашем билете написаны номер ряда и номер места. С помощью двух этих чисел мы легко находим свое место (рис. 2).
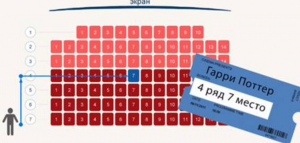
Рис. 2. Место в кинотеатре
Раньше дома не имели номеров. Вы приезжаете в город и ищете дом купца Елисеева. Когда людей и домов не очень много, то это не очень трудно. Особенно, если вы ищете дом известного человека (рис. 3).
Рис. 3. Дом без номера
Но в современном городе с сотнями тысяч и миллионами жителей ориентироваться нам помогает нумерация домов (рис. 4).
Рис. 4. Нумерация домов
Но вернемся к дороге. Представьте, что вы вдруг оказались на дороге перед отметкой 34 (рис. 5).

Рис. 5. Отметка 34
Понятно ли, где вы находитесь? Пока нет. Нужно знать еще вот что:
- В каких единицах это измерено: может, это километры, может, версты, а может, мы в Англии и это мили.
- Точка отсчета. А в какой стороне начало, город от которого отсчитывается? В какую сторону увеличиваются эти отметки?
Когда нам будут известны эти две вещи, то мы точно будем знать, где находимся.
Координатная (числовая) прямая
Моделью дороги в математике является прямая.
Две идеи (присвоить точкам имена и измерять расстояния) объединяются в одну – координатная (или числовая) прямая. Можно имена присваивать буквенные. Там даже функцию порядка можно сохранить – за A идет B, за B идет C и т.д. Но с измерением расстояний тут не понятно, как поступить. Поэтому удобнее присвоить точкам на прямой числовые имена.
Для этого требуется три действия.
- Отмечаем точку, относительно которой все будет считаться, начало отсчета. Самое разумное – поставить там отметку ноль, ведь если мы находимся в этой точке, то расстояние до начала отсчета равно нулю (рис. 6).

Рис. 6. Начало отсчета
- Выбираем единицы, в которых будем измерять. Для этого нужно указать длину отрезка, которую мы будем считать единичной (рис. 7).

Рис. 7. Единичный отрезок
- Выбираем направления, куда будут увеличиваться отметки. Отметим его стрелкой. Координатная прямая готова (рис. 8).
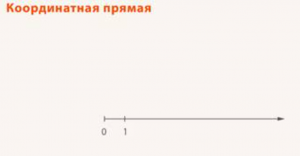
Рис. 8. Координатная прямая
Теперь каждой точке соответствует число, адрес этой точки. Это число называют координатой.
Модель дороги
Когда мы говорим «модель дороги в математике – прямая», может возникнуть резонный вопрос: но дорога далеко не всегда бывает прямой, она может быть какой угодно формы (рис. 9).
Рис. 9. Извилистая дорога
Уточним: мы говорим о модели дороги в том случае, если речь идёт не об удобстве, а только о расстоянии и порядке.
Если мы можем двигаться исключительно по дороге (не можем срезать и т.п.), то нам неважно, какой формы дорога: за столбом с номером 33 будет идти столб с номером 34 и т.д. Таким образом, для описания движения автомобиля, например, дорогу можно «выпрямить» и рассматривать модель – прямую
Координатная плоскость
В жизни мы часто сталкиваемся с ситуациями, когда упорядочивания по одному параметру недостаточно.
Например, в кинотеатре места занумерованы не от 1 до нескольких тысяч (что значительно усложнило бы поиск места зрителем), а обозначены номером ряда и номером места в этом ряду. Таким образом, каждому месту мы ставим в соответствие две координаты (а не одну) – ряд и место (рис. 10).
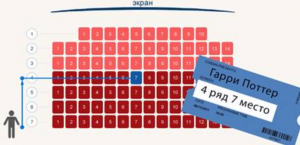
Рис. 10. Ряд и место
В этом случае нам уже не будет хватать координатной прямой, понадобится координатная плоскость.
Определение координат точки
Давайте потренируемся определять эти координаты для разных точек.
Определим координату точки A (рис. 11).

Рис. 11. Точка A
Для этого измерим, сколько раз единичный отрезок уложится от начала отсчета 0 до точки A. 4 раза. Точке A соответствует число 4. Или точка A имеет координату 4 (рис. 12).
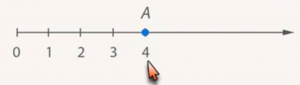
Рис. 12. Координата точки A
Иногда координату записывают в скобках после названия точки (рис. 13).
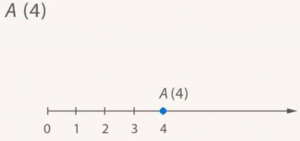
Рис. 13. Запись координаты
Определим координату точки B (рис. 14).
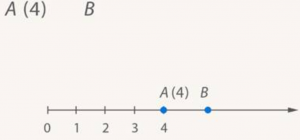
Рис. 14. Точка B
Единичный отрезок поместился 5,5 раз. Координата 5,5 (рис. 15).
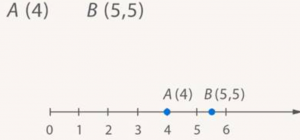
Рис. 15. Координата точки B
Можно поступить наоборот: найти точку по ее координате. Точка C имеет координату 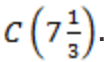 . Тогда от нуля нужно отложить 7 целых единичных отрезков и 1/7 (рис. 16).
. Тогда от нуля нужно отложить 7 целых единичных отрезков и 1/7 (рис. 16).
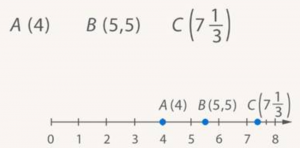
Рис. 16. Расположение точки
Пусть теперь точка левее начала отсчета. Точка D. Отрезок укладывается 4 раза. Но координата 4 уже занята для точки A справа (рис. 17).
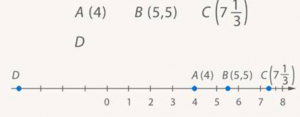
Рис. 17. Расположение точки D
Да и все остальные положительные числа уже использованы для координат тех точек, что находятся справа от нуля.
Но у нас остались еще отрицательные числа. Их и будем использовать для таких точек. То есть точка D имеет координату -4.
Две координаты, отличающиеся только знаками (то есть противоположные числа), соответствуют точкам, симметричным относительно начала координат. Например, 4 и -4 соответствуют двум симметричным точкам A и D (рис. 18).
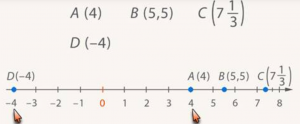
Названия числовых прямых
Когда имеется несколько числовых прямых, их различают с помощью букв, таких как , , и так далее. Например, в прямоугольной системе координат на плоскости присутствуют две оси, которые обычно обозначают как и . В данном случае, хотя прямая одна, её также часто обозначают буквой . Чтобы не откладывать единичные отрезки до нужной точки каждый раз, на прямой часто размещают отметки, соответствующие целым числам.
Определение
Таким образом, координатная прямая (или числовая прямая) представляет собой прямую, на которой определены начало отсчета, направление и масштаб (единичный отрезок).
Каждой точке на этой прямой соответствует определённое число, называемое координатой. Координата служит адресом для точки: зная её координату, можно точно определить местоположение точки, как по адресу можно найти дом. И наоборот, зная точку, можно точно сказать, какая у неё координата.
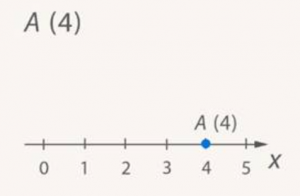
Рис. 19. Координатная прямая
Использование координатной прямой
Итак, когда же мы используем координатную прямую? Представьте, что вам по телефону нужно объяснить, где находятся эти точки на прямой (рис. 20).
![]()
Рис. 20. Точки на прямой
Мы можем взять линейку, измерить все расстояния между точками и передать по телефону.
А теперь, пусть это числовая прямая. Теперь у каждой точки есть координата, ее можно продиктовать по телефону, а на том конце ваш собеседник по этим координатам может точно так же расставить точки (рис. 21).
![]()
Рис. 21. Точки на координатной прямой
Сравнение чисел и арифметические операции с помощью числовой прямой
Итак, у нас каждой точке соответствует число и наоборот. Но соответствие распространяется и дальше – на сравнение чисел и на арифметические операции.
То, что 7,5 > 3, означает, что точка с большой координатой находится правее (рис. 22).
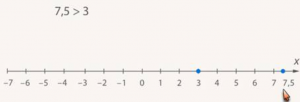
Рис. 22. Сравнение координат
Прибавить к числу 3 положительное число 2 на прямой будет означать, что от исходной точки с координатой 3 отступить вправо на 2 единичных отрезка. Придем в точку 5 (рис. 23).
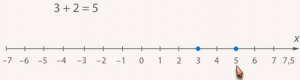
Рис. 23. Сложение положительных чисел
Прибавить отрицательное число (вычесть положительное) означает сдвиг влево (рис. 24).
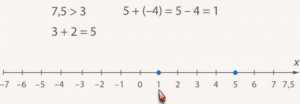
Рис. 24. Вычитание
Свойство противоположных чисел: их сумма равна нулю. Двум противоположным числам соответствуют симметричные относительно нуля точки. Например, -7 и 7. Можно к -7 прибавить 7, то есть сдвинуться на 7 единиц вправо, придем в точку ноль. Или, наоборот, от точки 7 можно сдвинуться на 7 единиц влево (прибавить отрицательное число -7 или вычесть 7) (рис. 25).
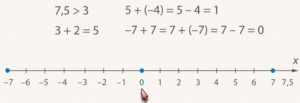
Рис. 25. Свойство противоположных чисел
Задача
Замена в задаче чисел точками, а сложения – сдвигом может облегчить решение. Чему равна сумма бесконечного числа слагаемых: 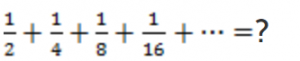
Решение
Изобразим точку 1/5 на прямой. Она находится посредине между 0 и 1 (рис. 26).

Рис. 26. Расположение точки 1/2
Добавить одну четвертую – значит найти точку, сдвинутую на ![]() единичного отрезка вправо, то есть на половину оставшегося до единицы (рис. 27).
единичного отрезка вправо, то есть на половину оставшегося до единицы (рис. 27).
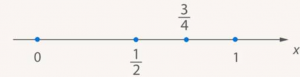
Рис. 27. Добавили 1/4
Добавим к нему 1/8, то есть еще движемся вправо на 1/8, половину оставшегося отрезка (рис. 28).

Рис. 28. Добавили 1/8
Этот процесс будет продолжаться до бесконечности, но новая точка всегда будет левее единицы, но все ближе и ближе к ней.
То есть сумма становится всё ближе к единице, но не превосходит ее. Поэтому такую бесконечную сумму считают равной единице: 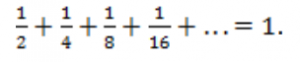
Заключение
В ходе нашего изучения мы пришли к выводу, что числовая прямая устанавливает взаимосвязь между точками и числами. Это взаимно-однозначное соответствие позволяет заменить работу с точками на работу с числами и наоборот. Переход от одних объектов к другим часто упрощает задачу и делает её более понятной.
Литература:
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. Ч. 2. М. «Просвещение», 2010.
- Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.
Дополнительные рекомендованные ресурсы в Интернете:
- Интернет-портал «math-prosto.ru» (Источник).
- Интернет-портал «school-assistant.ru» (Источник).
Домашнее задание:
Определите координату точки (рис. 1).
![]()
- На координатной прямой число -57 находится слева или справа от числа -42?
- Какую координату имеет точка, симметричная точке
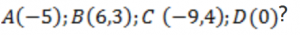 ?
?
Оцените урок:




