Введение

Посмотрите на эту картинку (Рис. 1). Это БелАЗ – один из самых больших карьерных грузовиков в мире.

Рис. 1. БелАЗ 

Но как понять, насколько он большой? Может это игрушка? (Рис. 2)

Рис. 2. Игрушечная машина

Или машина размером с трёхэтажный дом? (Рис. 3)

Рис. 3. Машина размером с трёхэтажный дом

Теперь давайте посмотрим на другую фотографию. Здесь уже можно сделать вывод о размерах грузовика – он раза в  выше взрослого человека, в  раза выше КамАЗа и т.д. (Рис. 4).

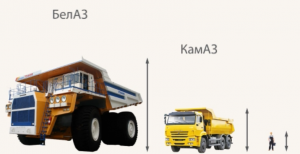
Рис. 4. Размеры БелАЗа в сравнении с КамАЗом и человеком

Теперь мы можем прикинуть его высоту: средний рост человека мы знаем – приблизительно  метр  сантиметров. Значит, высота грузовика чуть больше  метров (Рис. 5).

Рис. 5. Приблизительные размеры БелАЗа

Если вы найдёте в Интернете его характеристики, то убедитесь, что данная оценка очень близка к истине.

Какой вывод мы можем сделать? Для того чтобы по изображению можно было узнавать истинные размеры объекта, необходимо иметь какой-то эталон – объект, длину которого мы знаем. В нашем примере это был человек, рост которого мы знаем.

Что такое масштаб

Измерять высоту в людях, КамАЗах, машинах неудобно (потому что высота у людей, машин может быть разной). Поэтому лучше использовать универсальные единицы измерения (сантиметры, метры, километры) и прибор, позволяющий измерять размеры, например, линейку.

Измерим высоту линейкой – получилось 7 см (Рис. 6).

Рис. 6. Измеряем высоту БелАЗа

Если бы мы знали, сколько в 1 см на фотографии «настоящих» сантиметров, то легко посчитали бы высоту машины: если в 1 см на картинке 100 «настоящих» сантиметров (то есть на фотографии картинка уменьшена в 100 раз), то 7-сантиметровый грузовик в жизни окажется 700-сантиметровым, или 7-метровым (Рис. 7).

Рис. 7. Размеры БелАЗа

На самом деле только что мы научились измерять расстояния по карте. Действительно, если мы знаем, что на карте 1 см равен 5 км на местности (Рис. 8), то расстояние длиной 5 см на карте – это 25 км на местности (Рис. 9).

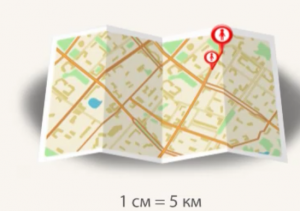
Рис. 8. 1 см = 5 км

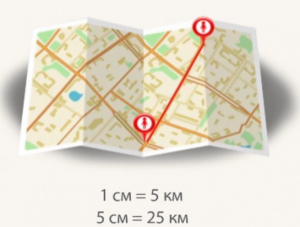
Рис. 9. 5 см = 25 км

Отношение размеров изображения к истинным размерам объекта назвали масштабом. Обозначают его буквой М. В нашем случае . Читается так: «масштаб 1 к 100».

Числитель дроби соответствует размеру изображения, а знаменатель – реальному размеру.

Запись  означает, что реальные размеры в 10000 раз больше нарисованных.

Запись масштаба в виде дроби практически не используют, и мы обычно его видим в таком виде: .

Обычно масштабом пользуются при чтении карт и чертежей домов или деталей.

Виды масштаба

Не всегда изображение меньше реального объекта. Чертеж может быть одинакового размера с деталью или большего размера (если деталь сама мелкая).

• Если масштаб меньше единицы (то есть изображение меньше реального объекта), то его называют масштабом уменьшения. Например: . Изображение в 10000 раз меньше реального объекта. Такой масштаб мы встречаем на картах, на чертежах домов или больших деталей, планах квартир.
• Если масштаб больше единицы (то есть изображение больше реального объекта), то его называют масштабом увеличения. Например: M = 10:1. Изображение в 10 раз больше реального объекта. Такой масштаб встречается при изображении мелких деталей и, например, насекомых.
• Если масштаб равен единице (то есть изображение по размеру равно реальному объекту) – М = 1:1, то говорят, что изображение выполнено в натуральную величину. Мы часто видим такой масштаб у манекенов в магазине. Их размер равен реальному размеру человека.

Использование масштаба

Вот две карты разного масштаба – города и страны (Рис. 10). Масштаб первой карты

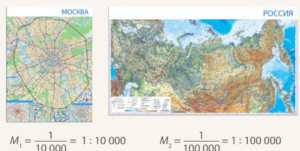
Рис. 10. Карты города и страны

Оба масштаба – это дроби. Так как в первом случае знаменатель меньше, то сам масштаб больше: .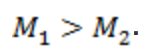

Для масштабов употребляют слова не «больше» и «меньше», а «крупнее» и «мельче». В данном случае крупнее, а  мельче.

Пример

На карте расстояние от города до деревни 23 см (Рис. 11). Масштаб карты 1:200 000. Найти истинное расстояние от города до деревни.

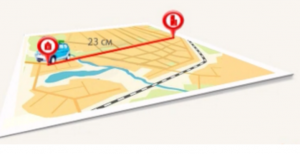
Рис. 11. Расстояние на карте

Решение

Такой масштаб означает, что реальный размер в 200 000 раз больше изображенного на карте.

Умножим измеренную длину на

Ответ: 46 км.

Для достаточно мелких масштабов (с большим знаменателем) после умножения получается очень большое число. Количество нулей мы уменьшаем, переводя сантиметры в метры или километры.

Иногда для нашего удобства этот перевод уже осуществлен. На карте можно увидеть такую запись: . Это не математическая запись (мы знаем, что 1 см не равен 2 км).

Чтобы вернуться к записи масштаба в виде отношения, нужно перевести километры в сантиметры:

Но пользоваться первой записью масштаба достаточно удобно.

Если на карте расстояние равно 4 см, то в реальности оно означает 8 км (Рис. 12).

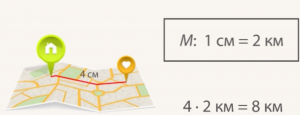
Рис. 12. Решение задачи с помощью первой записи масштаба

Задачи

Задача 1. Длина железной дороги Москва – Санкт-Петербург равна 650 км. Какой длины будет ее изображение на карте масштаба 1:10 000 000? (Рис. 13)

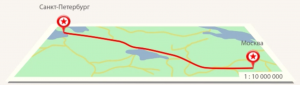
Рис. 13. Иллюстрация к задаче 1

Решение

Масштаб является уменьшающим. Изображение меньше реального в 10 млн раз. Поделим реальный размер на это число:

Ответ: 6,5 см.

Задача 2. Ширина детали равна 7 мм. Какова будет ее ширина на чертеже 

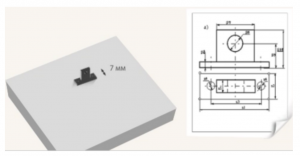
Рис. 14. Иллюстрация к задаче 2

Решение

Масштаб увеличивающий. Значит, ширина на чертеже будет в 20 раз больше: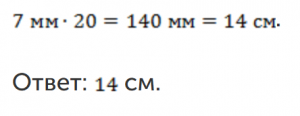

Заключение

Итак, повторим.

Масштаб – это отношение размера изображения к реальному размеру:

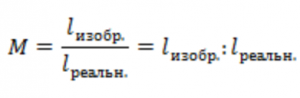
Если изображение меньше реального объекта, то масштаб уменьшающий. Числитель у него – единица, а знаменатель показывает, во сколько раз изображение уменьшено. Чем больше знаменатель, тем мельче масштаб

Если изображение больше реального объекта, то масштаб увеличивающий. Знаменатель – единица, а числитель показывает, во сколько раз изображение увеличено. Чем больше числитель, тем крупнее масштаб

Представим следующую ситуацию. Длина детали 5 см, а на чертеже получилось 2 см. Это будет означать, что М = 2 : 5. Или длина детали 4 см, а на изображении – 20 см. Тогда М = 20 : 4. Вопрос: почему мы не сталкиваемся с такими записями масштабов? Ведь могут встретиться такие размеры? Да, могут. И такой масштаб можно было бы указать, но тогда он стал бы сложнее для перевода. Такие дроби сокращают, чтобы или числитель, или знаменатель был равен 1. Получаем, что .

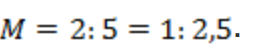
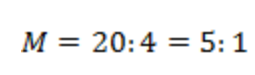
В качестве домашнего задания попробуйте составить план своей комнаты в масштабе 1 : 50. Кроме самой комнаты, начертите свою кровать, стол, шкаф.