Модуль числа
Определение модуля числа
В алгебре существует четкое определение модуля числа. Модуль числа в математике представляет собой расстояние от начала координат до точки на координатной прямой, соответствующей этому числу.
Если мы обозначим некоторое число «a» и изобразим его на координатной прямой точкой A, то расстояние от точки A до начала координат (то есть до нуля) будет называться модулем числа «a».
Обозначение модуля выглядит так: |a| = OA.
Рассмотрим это на примере:
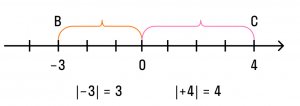
Точка B, соответствующая числу -3, располагается на расстоянии трех единиц от точки O (начала координат). Это означает, что длина отрезка OB составляет 3 единицы.
Число 3 называется модулем числа -3, и его можно записать следующим образом: |−3| = 3 (что читается как «модуль числа минус три равен трём»).
Точка C, соответствующая числу +4, находится на расстоянии четырех единиц от начала координат, следовательно, длина отрезка OC равна четырем единицам.
Число 4 является модулем числа +4 и обозначается так: |+4| = 4. Плюс можно опустить, и запись будет выглядеть как |4| = 4.
Онлайн-курсы математики для детей помогут улучшить успеваемость, подготовиться к контрольным, ВПР и экзаменам.
Получите больше преимуществ от Skysmart:
- Углубляйте свои знания на курсах математики.
- Выбирайте из более чем 1200 репетиторов по математике.
- Записывайтесь на бесплатные курсы для детей.
Свойства модуля числа
Рассмотрим семь основных свойств модуля. Эти правила будут полезны независимо от того, в каком классе учится ребенок.
Модуль числа представляет собой расстояние, и так как расстояние не может быть отрицательным, модуль числа также не может быть отрицательным: |a| ≥ 0.
Модуль положительного числа равен самому числу: |a| = a, если a > 0.
Модуль отрицательного числа равен положительному значению этого числа: |−a| = a.
Модуль нуля равен нулю: |0| = 0.
Противоположные числа имеют одинаковые модули: |−a| = |a| = a.
Модуль произведения равен произведению модулей этих чисел: |a·b| = |a|·|b|, если a·b = 0 или a·b < 0.
Модуль частного равен частному от деления модуля числителя на модуль знаменателя: |a/b| = |a|/|b|.
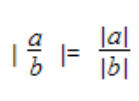
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
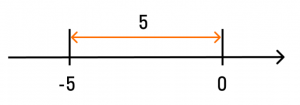
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой или длине отрезка АВ.
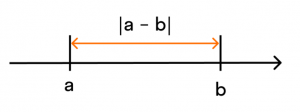
Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.
Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.
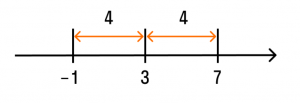
Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.
Решим неравенство: |a + 7| < 4.
Эту запись читаем так: расстояние от точки a до точки −7 меньше четырех. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:
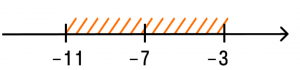
Ответ в данном случае будет таким: (−11; −3).
Решим неравенство: |10 − x| ≥ 7.
Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.
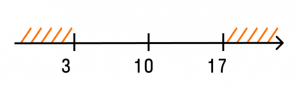
Ответ: (−∞; 3] [17, +∞).
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Для x < 0 имеем y = −x. В результате получаем:
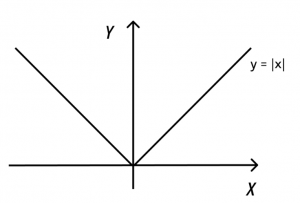
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
В контрольной работе или на ЕГЭ может встретиться задачка, в которой нужно вычислить √a2 , где a – некоторое число или выражение.
При этом, √a2= |a|.
По определению арифметического квадратного корня √a2 — это такое неотрицательное число, квадрат которого равен a2 .
Оно равно a при а > 0 и −а, при а < 0 , т. е. как раз |a|.
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
|-3,5| = 3,5
|2,27| = 2,27
![]()
Оцените урок:





