Введение

Нам часто в жизни приходится находить дробь от числа.

Четверть часа – это что такое? Это 1/4 от 60 минут. Это будет 15 минут.

А три четверти часа? Это в 3 раза больше, чем одна четверть. 3 раза по 15 минут, 45 минут.

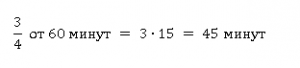
2/3 полуторалитровой бутылки молока – сколько это? Одна треть – пол-литра, 2 трети – литр.

В этом уроке не нужно изучать ничего нового. Чтобы найти дробь от числа, нужно умножить эту дробь на это число. Есть два типа чисел, на которые можно умножать дроби: целые и дробные. Большой разницы нет, но давайте рассмотрим оба случая отдельно.

Умножение целого числа на дробь

1. Найти 1/7 от 63

Умножить на 1/7 – означает разделить на 7.

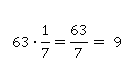
2. Найдем 5/7 от 63.

Надо умножить 63 на 5/7.

Здесь очень много вариантов, как можно рассуждать.

Вариант 1.

Можно вспомнить, что 5/7 – это 5 раз по 1/7, то есть .

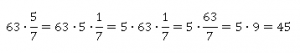
Вариант 2.

Можно вспомнить формальное правило. Чтобы дробь умножить на число, надо числитель умножить на это число.

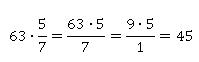
Вариант 3.

Можно представить 63 в эквивалентном виде как дробь и уже пользоваться правилом умножения дробей. Числитель умножить на числитель, знаменатель – на знаменатель.

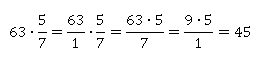
Вариант 4

Самая короткая запись получится, если вспомнить, что число, которое мы умножаем на дробь, можно сокращать со знаменателем.

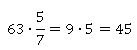
Все это одно и то же. Поступайте так, как вам удобнее.

Умножение дроби на дробь

Найдем теперь дробь от дробного числа, то есть от другой дроби.

1. Найти 2/5 от 15/8.

Умножаем:

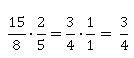
Очевидно, что 2/5 от 15/8 и 15/8 от 2/5 равны друг другу. Ведь это произведение двух этих чисел, которое не зависит от порядка множителей.

Умножение десятичной дроби на целое число

Найдем 0,03 от 45.

0,03 мы можем записать в эквивалентном виде как обыкновенную дробь и выполнить умножение.

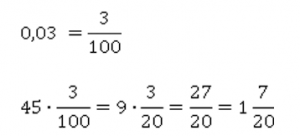
Но десятичная запись удобна сама по себе, и выполнить действия можно сразу.

45 умножаем на 3 и запятой отделяем две цифры:

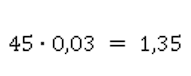
Это дело вкуса и конкретных чисел. Иногда удобнее одна запись, иногда другая.

Проценты

Мы знаем еще одно обозначение дробей, проценты.

1. Найти 35 % от 400.

1 % – это 1 сотая, 35 % – это 35 сотых.

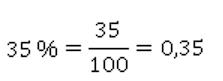
Эти сотые мы можем записать обыкновенной дробью или десятичной.

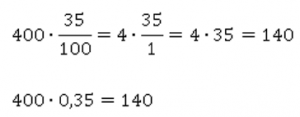
Задание

Самостоятельно выполните следующие задания:

Найти:

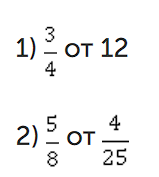
3) 0,2 от 0,8

4) 30 % от 50

5) 65 % от

Проверяем:

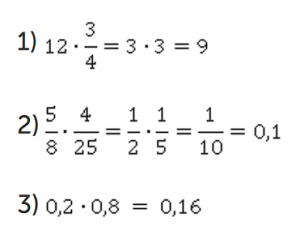
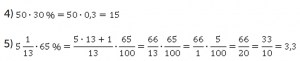
Заключение

Таким образом, для того чтобы определить дробь от числа, будь то целое или дробное, необходимо умножить это число на соответствующую дробь.

Список литературы

1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А. Г., Полонский В. В., Якир М. С. Математика для 6 класса. – Гимназия, 2006.
3. Депман И. Я., Виленкин Н. Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А. Н., Чайковский И. В. Задания по курсу математики для 5-6 классов. – ЗШ МИФИ, 2011.
5. Рурукин А. Н., Сочилов С. В., Чайковский К. Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
6. Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика: учебник-собеседник для 5-6 классов. – М.: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные онлайн-ресурсы

• Интернет-ресурс «school-assistant.ru» (Источник)
• Интернет-ресурс «math-prosto.ru» (Источник)

Домашнее задание

Для выполнения домашнего задания используйте Математика 6 под редакцией Виленкина Н. Я., Жохова В. И., Чеснокова А. С., Шварцбурда С. И. (М.: Мнемозина, 2012). Задания: № 486 (а, г, ж, к), № 500, № 526, № 495, № 531.