Поиск наибольшего общего делителя (НОД) с помощью алгоритма Евклида

Наибольший общий делитель (НОД) двух чисел можно определить различными методами. В этом уроке мы рассмотрим алгоритм Евклида, который существует в двух вариантах: с вычитанием и с делением. Примеры помогут глубже понять и закрепить новый материал.

Введение в понятие НОД

Наибольший общий делитель — это наибольшее число, на которое делятся два или более натуральных чисел без остатка. Например, если у нас есть числа 48 и 36, то НОД этих чисел — это максимальное число, которое делит оба числа.

Пример 1

Предположим, у нас есть 48 шоколадок и 36 конфет. Мы хотим составить подарочные наборы, чтобы каждому ребенку досталось одинаковое количество шоколадок и конфет.

Чтобы определить, сколько наборов мы можем сделать, нам нужно найти НОД чисел 48 и 36.

Делители:

• 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
• 36: 1, 2, 3, 4, 6, 9, 12, 18, 36

Общие делители: 1, 2, 3, 4, 6, 12.

Наибольший общий делитель — 12. Значит, мы можем сделать 12 наборов, в каждом из которых будет по 4 шоколадки и 3 конфеты.

Определение НОД

Наибольший общий делитель (НОД) двух и более натуральных чисел — это наибольшее натуральное число, которое делит каждое из данных чисел. Например, НОД(48; 36) = 12.

Свойства НОД

1. У любых двух чисел есть хотя бы один общий делитель — это число 1.
2. Два числа называются взаимно простыми, если их НОД равен 1. Например, 2 и 3, 3 и 7 — взаимно простые числа.
3. 
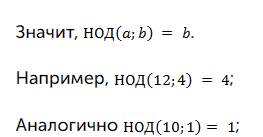
4. Если одно число делится на другое, то НОД равен большему числу.

Метод разложения на множители

Для нахождения НОД можно использовать метод разложения на простые множители.

Пример 2

Найдем НОД для чисел 36 и 48:

• 36 = 2² × 3²
• 48 = 2⁴ × 3¹

Общие множители: 2² и 3¹. Перемножив их, получаем НОД = 2² × 3¹ = 12.

Алгоритм Евклида

Если разложение на множители затруднено, можно использовать алгоритм Евклида. Он основан на следующем принципе: если у нас есть два числа, мы можем заменить большее из них на их разность, и НОД не изменится.

Пример 3

Найдем НОД(48; 36) с помощью алгоритма Евклида:

1. 48 — 36 = 12
2. 36 — 12 = 24
3. 24 — 12 = 12
4. 12 — 12 = 0

Когда одно из чисел становится равным 0, другое число и есть НОД. В данном случае НОД(48; 36) = 12.

Заключение

Сегодня мы познакомились с понятием наибольшего общего делителя, его свойствами и методами нахождения. Мы рассмотрели три способа: выписывание делителей, разложение на множители и алгоритм Евклида. Понимание НОД будет полезно при работе с дробями и в других математических задачах.

Рекомендованное домашнее задание

1. Найдите НОД чисел: 27, 15 и 9.
2. Найдите НОД(424; 477) с помощью алгоритма Евклида.
3. Туристы проехали за первый день 56 км, а за второй — 72 км, причем их скорость была целым числом км/ч. Найдите максимальную скорость, с которой ехали туристы, если они были в пути целое число часов.