Приведение дробей к общему знаменателю
На этом уроке мы изучим, как приводить дроби к общему знаменателю, находить наименьшее общее кратное (НОК) и наименьшее общее значение (НОЗ) с помощью разложения на простые множители. Эти навыки помогут нам сравнивать дроби с разными знаменателями, а также вспомнить, как сравнивать дроби с одинаковыми знаменателями.
Если у вас возникнут трудности с пониманием темы, рекомендуем обратиться к уроку «Часть 2. Дроби. Рациональные числа».
Сравнение дробей с разными знаменателями
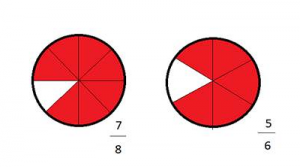
Рассмотрим, как сравнить две дроби с разными знаменателями. На рисунке видно, что одна дробь может выглядеть больше другой, но давайте проверим это математически. Для начала вспомним, что при сравнении дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
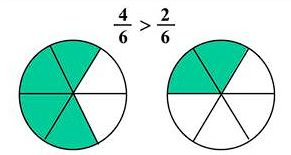
Сравнение дробей с разными знаменателями через нахождение НОК и НОЗ
Значит, для того чтобы сравнить две дроби с разными числителями и знаменателями, нам нужно привести их к общему знаменателю. Как же это сделать? Вернемся к нашим дробям 7/8 и 5/6 и воспользуемся основным свойством дробей. Нам нужно умножить и числитель, и знаменатель на одно и то же число и получим дробь, равную данной. Давайте умножим числитель и знаменатель первой дроби на знаменатель второй. А потом числитель и знаменатель второй дроби на знаменатель первой. (6 и 8 – дополнительные множители). Теперь у нас есть две дроби с одинаковыми знаменателями и мы можем их сравнить.
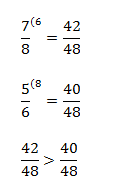
Учитываем уже знакомое нам правило, что из двух дробей с одинаковыми знаменателями больше та, числитель которой больше.
Давайте рассмотрим другой способ приведения к общему знаменателю, его удобнее использовать в случае, если знаменателями выступают очень большие числа. Он основан на определении общего знаменателя дробей.
Возьмем уже знакомую нам пару дробей 7/8 и 5/6. Для того чтобы найти общий знаменатель, нам нужно найти наименьшее общее кратное для 8 и 6. НОК (6;8) = 24, значит, и обе дроби нам нужно привести к знаменателю 24.
Чтобы привести дробь 7/8 к знаменателю 24, ее нужно умножить на 3. Дробь 5/6 – на 4.
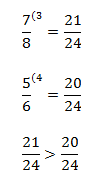
Приведение дробей к общему знаменателю
Найдите наименьшее общее кратное (НОК). Для этого определите НОК знаменателя этих дробей, который является НО исходной дроби. Определите дополнительный множитель каждой дроби. Умножьте числитель и знаменатель исходной дроби на соответствующий дополнительный множитель.
Нахождение НОК для дробей с большими знаменателями
Если знаменатели дробей большие, более удобным способом будет нахождение наименьшего общего кратного (НОК). Например, для дробей с знаменателями 6 и 8, НОК будет равен 24. Соответственно, мы можем привести дроби к этому знаменателю.
Чтобы привести дробь a66a к знаменателю 24, нужно умножить её на 4, а дробь b88b – на 3.
Примеры решения задания, употребление разложения числа на простые множители для нахождения НОК
Привести к общему знаменателю дроби 3/14 5/21.
Решение
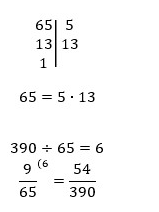
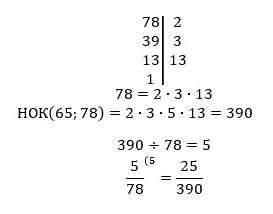
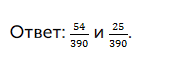
Не всегда легко можно подобрать НОК чисел, и в таком случае вам поможет умение раскладывать числа на произведение простых множителей.
Задание
Привести к общему знаменателю дроби 9/56 и 5/78.
Решение
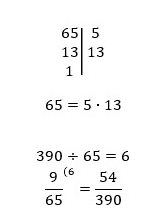
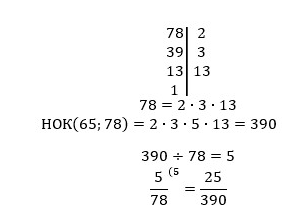

Итоги урока
Мы научились приводить дроби к общему знаменателю и использовали разложение на простые множители для нахождения НОК.
Список литературы
- Виленкин Н.Я. Математика. 6 класс. Учебник. – 2014.
- Никольский С.М., Потапов М.К. Математика. 6 класс. Учебник. – М.: 2012.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 6 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Домашнее задание
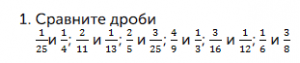
Дополнительные ресурсы
- Интернет-портал «math-prosto.ru»
- Интернет-портал «school-assistant.ru»
Оцените урок:




