Сегодня мы изучим, как находить наименьшее общее кратное (НОК) нескольких чисел. Для начала вспомним, что такое взаимно простые числа, а также определим понятия НОД (наибольший общий делитель) и НОК, и рассмотрим их свойства. Это поможет вам самостоятельно и уверенно применять полученные знания на практике.

Определение

Кратное числа $n$ — это число, которое делится на $n$ без остатка.

Например, существуют вещи однократного использования, такие как одноразовая посуда, и вещи многократного использования — например, фотоаппарат или компьютерная игра.

Примеры № 1

Кратные числа можно получить, повторяя одно и то же действие несколько раз. Например, кратные числа для 3: 3 (один раз), 6 (два раза), 9 (три раза). Для 15 кратные числа будут: 15, 30, 45 и так далее. Все эти числа делятся на свои делители: в первом случае — на 3, во втором — на 15.

Наименьшее общее кратное

Наименьшее общее кратное (НОК) для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.

Примеры № 2

Найдем НОК для следующих чисел: 1. 15 и 21; 2. 42 и 70.

Решение

1. Сначала найдем кратные числа для 15: 15, 30, 45, 60, 75, 90, 105 и так далее.
   Кратные числа для 21: 21, 42, 63, 84, 105, 126, 147 и так далее.
   Общее кратное для 15 и 21 — это 105. Таким образом, НОК(15, 21) = 105.

1. Для 42 кратные числа: 42, 84, 126, 168, 210 и так далее.
   Кратные числа для 70: 70, 140, 210, 280 и так далее.
   Наименьшее общее кратное здесь — 210.

Хотя этот метод работает, он может быть не самым эффективным. Поэтому для более рационального поиска НОК мы будем разлагать числа на простые множители.

Примеры № 3

Найдем НОК для следующих пар чисел: 1. 72 и 84; 2. 129 и 240; 3. 129 и 40; 4. 21 и 25; 5. 2 и 7.

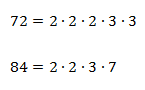
Решение

1. Разложим 72 и 84 на простые множители:

   Чтобы число делилось на 72, оно должно содержать три двойки и две тройки, а для деления на 84 — две двойки, одну тройку и одну семерку.
   Мы выписываем все простые множители, добавляя недостающие:

   НОК(72,84)=23⋅32⋅7=504.НОК(72,84)=23⋅32⋅7=504.

2. Аналогично разложим 129 и 240:

   • $129=3\cdot 43$
   • 240=24⋅3⋅5240=24⋅3⋅5

   Соберем все множители:

   НОК(129,240)=24⋅3⋅5⋅43=2580.НОК(129,240)=24⋅3⋅5⋅43=2580.

3. Для 129 и 40:

   • 40=23⋅540=23⋅5

   Получаем:

   НОК(129,40)=23⋅5⋅3⋅43=2580.НОК(129,40)=23⋅5⋅3⋅43=2580.

4. Для 21 и 25:

   • $21=3\cdot 7$
   • 25=5225=52

   Взаимно простые числа, следовательно:

   НОК(21,25)=3⋅7⋅52=315.НОК(21,25)=3⋅7⋅52=315.

5. Для 2 и 7:
   Взаимно простые числа:

   $$\text{НОК}(2,7)=2\cdot 7=14.$$

Определение

Наименьшее общее кратное чисел $a$ и $b$ — это наименьшее число, которое делится и на $a$, и на $b$.

Связь НОК и НОД

Существует интересное свойство, связывающее НОК и НОД: если НОК чисел $a$ и $b$ умножить на НОД этих чисел, то получится то же самое, что и просто умножить $a$ на $b$:

Пример

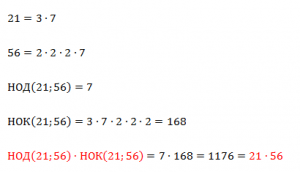
Список литературы

1. Виленкин Н.Я. и др. «Математика. 6 класс. Учебник для общеобразовательных учреждений». – 30-е изд., Мнемозина, 2013.
2. Зубарева И.И., Мордкович А.Г. «Математика, 6 класс». – М.: Мнемозина.
3. Истомина Н.Б. «Математика, 6 класс». – М.: Ассоциация XXI век.

Дополнительные ресурсы

• Интернет-портал «math-prosto.ru»
• Интернет-портал «school-assistant.ru»
• Интернет-портал «fxyz.ru»

Домашнее задание

1. Найдите НОК для чисел:
   а) 30 и 42
   б) 16 и 18
   в) 13 и 19
   г) 127 и 319
   д) 2 и 9

2. Определите, что такое взаимно простые числа.

3. Объясните, что такое НОД и НОК и какое у них общее свойство.