Противоположные числа

Радость и грусть, активность и усталость — это противоположные эмоции, знакомые каждому из нас. Но не все шестиклассники знают, что такое противоположные числа.

Определение противоположных чисел

В шестом классе каждый ученик должен познакомиться с понятием противоположных чисел. Давайте начнем с построения координатной прямой.

Координатная ось представляет собой прямую линию, на которой обозначено начало координат, установлен единичный отрезок и направлена стрелка, указывающая положительное направление.

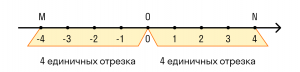
Точки M(-4) и N(4) находятся на одинаковом расстоянии от точки O, но расположены по разные стороны от нее, в противоположных направлениях. Поэтому числа -4 и 4 считаются противоположными.

Противоположными числами называют такие числа, которые соответствуют точкам на координатной прямой, находящимся на равном расстоянии от начала отсчета, но в разных направлениях (положительном и отрицательном). Нуль, в свою очередь, находится в начале отсчета и является противоположным сам себе.

Примеры пар противоположных чисел:

1 и -1;
0,25 и -0,25;
88,158 и -88,158;
2/7 и -2/7.

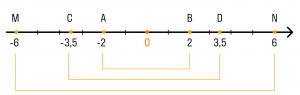
Целые числа включают в себя натуральные числа, их противоположные (отрицательные) значения и ноль.

Обозначение противоположных чисел

Противоположные числа имеют свои обозначения. Чтобы записать число, противоположное данному, используется знак минус: «-».

Противоположные числа — это пара чисел, которые различаются только знаком.

Иными словами, если t — это число, то его противоположное значение обозначается как -t. Например:

• Если t = -13, то противоположное ему -t = 13.
• Если t = 0,123, то его противоположное -t = -0,123.
• Если t = 0, то его противоположное -t = 0.

Запись -(-t) обозначает число, противоположное -t. Например, -(-0,09) = 0,09. Таким образом, число, противоположное -0,09, — это 0,09.

-1809 и 1809;
√202 и -√202;
-20 и -(-20).

Примеры противоположных рациональных чисел:

1,121 и -1,121;
0,(5678) и -0,(5678).

Также противоположными могут быть иррациональные числа, такие как значения выражений, например, (√4 + 2) и -(√4 + 2).

Свойства противоположных чисел

Рассмотрим основные характеристики противоположных чисел:

1. Для каждого действительного числа существует единственное число, которое ему противоположно. Это связано с тем, что для каждой точки на координатной оси есть только одна точка, симметричная ей относительно нуля.

2. Противоположные числа имеют разные знаки: одно из них положительное, а другое — отрицательное. Это свойство объясняется тем, что такие числа располагаются по разные стороны от нуля на координатной оси. Исключение составляет ноль (0), который является противоположным сам себе.

Таким образом, если число имеет положительный знак, то его противоположное значение будет отрицательным, и наоборот.

3. Свойство симметрии: если число a является противоположным числу b, то b также является противоположным a.

4. Модули противоположных чисел равны. Точки на координатной прямой, соответствующие противоположным числам, находятся на одинаковом расстоянии от нуля.

5. Сумма противоположных чисел всегда равна нулю: n + (-n) = n — n = 0. Это означает, что такие числа равны по модулю, но имеют противоположные знаки.

Например, сумма противоположных чисел 101 и -101 равна 0, так же как и результат сложения √5 и -√5, который также равен нулю.

Задания для самопроверки

Назовите число, противоположное следующим:

• 20 472;
• −15;
• −0,3;
• √1048;
• 0