Длина окружности. Площадь круга
На этом уроке вы вспомните понятия окружности и круга, а также изучите их основные элементы. Кроме того, вы познакомитесь с числом π и двумя новыми формулами: формулой для вычисления длины окружности и формулой для площади круга, а также научитесь применять их при решении различных задач.
Если у вас возникнут трудности с пониманием темы, рекомендуем ознакомиться с уроком «Точность и округление».
Введение
Как вы уже знаете, многие объекты имеют форму круга. Почему это так?
Рассмотрим, например, колесо. Очевидно, что круглое колесо катится гораздо легче, чем квадратное. Или, скажем, стакан круглой формы гораздо удобнее держать в руке, чем стакан с прямыми углами. Таким образом, человечество в какой-то момент начало использовать круглые предметы. Однако, используя их, необходимо научиться их измерять. Например, вам нужно знать длину окружности стакана, чтобы понять, сколько материала потребуется для его изготовления, или вам нужно знать площадь колеса, чтобы определить, сколько исходных материалов нужно для его создания.
Поэтому сегодня мы обсудим, как находить длину окружности и площадь круга, а также решим несколько задач, связанных с этими понятиями.
Окружность и круг
Для начала давайте вспомним, что такое окружность и круг.
Окружность — это множество всех точек на плоскости, которые находятся на равном расстоянии от заданной точки.
То есть, если мы возьмем некоторую точку и зададим определенное расстояние — радиус окружности — то окружность будет состоять из всех точек, находящихся на этом расстоянии от исходной точки (см. Рис. 1).
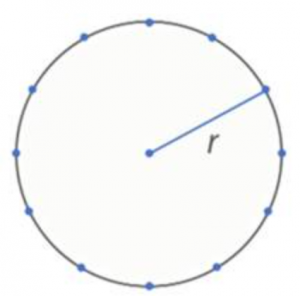
А теперь вспомним еще два важных понятия (см. Рис. 2).
Хордой называется такой отрезок, которые соединяет любые две точки, лежащие на окружности.
Диаметр – это такая хорда, которая проходит через центр окружности. Соответственно, как следствие, нетрудно догадаться, что диаметр равен двум радиусам.
![]()
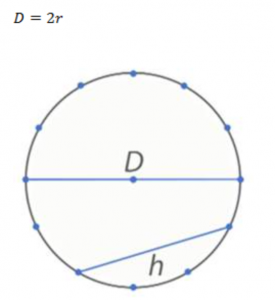
Рис. 2. Хорда и диаметр
Круг – это все точки на плоскости, которые лежат внутри окружности, а также сама окружность (см. Рис. 3).

Рис. 3. Круг

Длина окружности
Теперь, когда мы вспомнили основные определения, давайте обсудим, как измерить длину окружности.
Один из предложенных способов заключается в следующем: возьмем стакан с круглым дном и обмотаем его основание ниткой. После этого мы сделаем отметку на нитке в месте, где её конец совпадет с началом. Затем размотаем нитку и измерим её длину с помощью линейки. Конечно, это измерение не будет абсолютно точным, так как оно зависит от аккуратности наших действий, а также от точности используемой линейки и других факторов. Тем не менее, с помощью этого метода мы сможем примерно определить длину окружности (см. Рис. 4).

Рис. 4. Способ измерения длины окружности
Конечно же, чем дальше человечество продвигалось по своим научным взысканиям, тем более точно оно могло измерить эту самую длину окружности.
Еще в древности люди заметили, что если вы увеличите радиус окружности, например в два раза, то и длина этой окружности увеличится в два раза. Если уменьшить радиус в три раза, то и длина уменьшится в три раза. Иначе говоря: длина окружности и ее радиус пропорциональны друг другу. То есть их отношение – это постоянное число (см. Рис. 5).
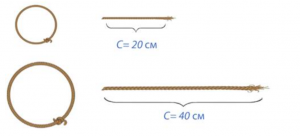
Рис. 5. Иллюстрация пропорциональности длины окружности и радиуса
Так как отношение длины окружности к радиусу – постоянное число, то и отношение длины к диаметру – постоянное число.
Итак, пусть длина окружности C, а диаметр окружности – d. Так как отношение длины к диаметру всегда постоянное, то его можно примерно посчитать. Проделав это, вы примерно получите число 3,1415926…. Так как число, которое равно отношению длины окружности к ее диаметру, не могли посчитать точно, его обозначили специальной буквой, буквой π (буква греческого алфавита).

Сейчас, благодаря мощным компьютерам, можно вычислить тысячи и даже миллионы знаков числа π. Это позволяет более точно определять длину окружности. Однако для практических нужд достаточно всего лишь нескольких первых знаков: 3,14.
Существует несколько методов, помогающих запомнить число π. Один из них — это стихотворение:
Если очень постараться,
То запомнишь все как есть.
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Есть и другой интересный способ, который также помогает запомнить несколько знаков числа π.
Я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Если посчитать количество букв в каждом слове, то получится 3,14159265358.
Таким образом, мы создали более длинный ряд. На самом деле существуют и более длинные стихотворения, которые помогают запомнить число π. Некоторые даже устраивают чемпионаты, например, чемпионат мира по запоминанию знаков числа π.
Теперь вернемся к нашей теме.

Используя данную формулу, мы можем практически точно вычислить длину любой окружности, так как диаметр можно измерить с помощью линейки. Умножив диаметр на число π, мы получим искомую длину. Хотя значение числа π не является абсолютно точным, для приблизительных расчетов достаточно использовать его с точностью до сотых или тысячных. При этом, если вы подставите в расчет значение π, например, 3,14 или 3,1415, длина будет лишь приблизительной, поэтому вместо знака равенства следует использовать знак приблизительного равенства. Для точного результата лучше оставить в ответе символ π, что будет правильным ответом.
Теперь рассмотрим конкретные примеры, чтобы проиллюстрировать этот процесс.
Пример 1
Дана окружность с радиусом 2 сантиметра. Какова ее длина?

Как видите, тут мы использовали знак приблизительного равенства.
Пример 2
Диаметр окружности равен 3 см, чему равна длина этой окружности?
Решение:
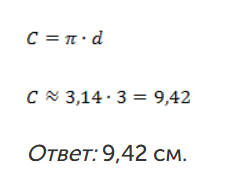
Можно было записать ответ в виде: ![]() .
.
В этом случае мы можем поставить знак равенства, ведь значение абсолютно точное. Другой вопрос, что для практических целей оно не совсем удобно. Но так как математика – точная наука, то точным ответом будет ![]() .
.
Между прочим, формулу 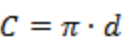 можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде
можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде
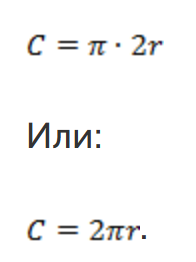
Площадь круга
Давайте рассмотрим, как наши предки вычисляли площадь круга. Существовал один метод, позволяющий приблизительно определить эту площадь.
Представим себе круг и заметим, что его площадь меньше площади квадрата, который его описывает. Площадь этого квадрата легко вычислить, возведя в квадрат длину его стороны.
Кроме того, мы можем улучшить наше приближение к кругу, обрезая углы квадрата. В результате получится фигура, площадь которой ближе к площади круга. Этот процесс можно продолжать бесконечно, постепенно уточняя приближение (см. Рис. 6).
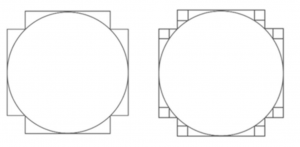
Рис. 6. Приблизительное вычисление площади круга
Естественно, что точно так же мы можем сделать, если мы нарисуем квадрат внутри круга, после чего добавим такие прямоугольники со всех сторон и т. д., пока мы сколь угодно близко не приблизимся к площади искомого круга (см. Рис. 7).
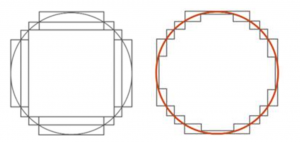
Рис. 7. Приблизительное вычисление площади круга
Площадь круга мы можем оценить как сверху (площадь круга будем меньше, чем площадь фигуры, которая описывает круг), так и снизу (площадь круга больше, чем площадь фигуры, вписанной в эту окружность). Соответственно, если прямоугольников, которыми мы измеряем, будет довольно много, то мы сможем приблизительно оценить площадь круга.
В девятом классе вы докажете формулу, что на самом деле площадь круга s вычисляется так: 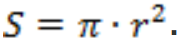 .
.
Примеры на вычисление площади круга
Пример 1
Найдите площадь круга, если его радиус равен 1 см.
Решение:
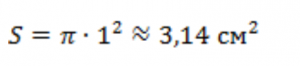
Можно записать ответ в виде ![]() либо же подставить число π и получить приблизительное значение.
либо же подставить число π и получить приблизительное значение.
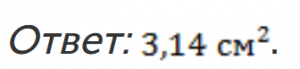
Пример 2
Найдите площадь круга, если диаметр круга равен 4 см.
Решение:
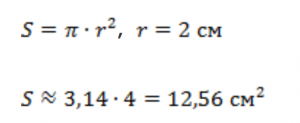
Или же можем записать этот ответ точно, через π.
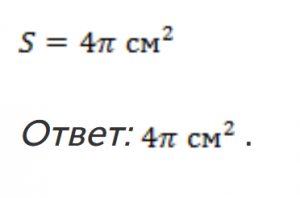
Оцените урок:





