Введение

Когда мы видим очень высокого человека, нам может прийти в голову, что он баскетболист. Если мы наблюдаем большой камень, мы можем предположить, что его невозможно поднять из-за его веса. Аналогично, глядя на число, мы можем сразу понять, что оно делится на другое число.

Во всех этих случаях мы не проводили проверки, а делали выводы на основе внешних признаков. В первых двух примерах возможны ошибки, но в случае с числами это работает иначе: если последняя цифра числа делится на 5, значит, и всё число делится на 5.

В математике существуют точные признаки делимости для различных чисел. Например, легко определить, делится ли число на 2 или на 3. Но также существует быстрый способ выяснить, делится ли число на 9 или на 3, основываясь на сумме его цифр. Если сумма цифр числа делится на 9, то и само число делится на 9.

Признаки делимости

Начнем с определения: что значит, что одно число делится на другое? Например, число A делится на B, если A можно представить в виде произведения двух натуральных чисел, одно из которых — B. Это также означает, что A содержит B как множитель.

Если A делится на B, то можно записать это как A = B × C, где C — результат деления A на B.

Основная теорема арифметики

Разложим число на множители. Мы можем продолжать разложение до тех пор, пока не получим простые числа, которые не могут быть разложены дальше. Простые числа — это такие, которые делятся только на 1 и на себя. Составные числа, такие как 4, 6 и 8, можно разложить на множители. Единица же не считается ни простым, ни составным числом.

Основная теорема арифметики утверждает, что любое число можно единственным образом представить в виде произведения простых множителей. Это означает, что независимо от того, как мы раскладываем число на множители, в итоге мы получим одно и то же разложение (возможно, в разном порядке).

Деление нуля и деление на нуль

Когда число A делится на B? Это происходит, когда A содержит B как множитель. Например, 0 можно записать как 0 × C, что демонстрирует, что 0 делится на любое ненулевое число.

Однако деление на нуль невозможно. Если бы мы могли разделить число на 0, то возникло бы противоречие, так как результат деления не мог бы быть определён. Поэтому деление на ноль не имеет смысла и не требуется.

Делимость чисел, оканчивающихся на 0

Если число оканчивается на 0, это означает, что оно содержит множитель 10. Например, число 50 можно представить как 5 × 10, что подтверждает его делимость на 10, 5 и 2.

Делимость суммы

Рассмотрим два случая:

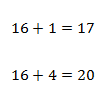
1. Если одно слагаемое делится на число, а другое — нет, то сумма не делится на это число.
2. Если оба слагаемых делятся на одно и то же число, то и их сумма также делится на это число.

Таким образом, если все слагаемые делятся на одно число, то и сумма делится на это число. Однако если несколько слагаемых не делятся на одно и то же число, то результат может быть различным.

Пример

Рассмотрим большое число, например, 1234567890, и определим, на какие числа оно делится. Мы можем представить его как сумму:

1. Первое слагаемое оканчивается на 0, значит, оно делится на 10, 5 и 2.
2. Если второе слагаемое не делится на 10, то вся сумма не делится на 10.

Теорема (признак делимости на 2, 5 и 10)

Число делится на 2, 5 или 10 тогда и только тогда, когда его последняя цифра делится на 2, 5 или 10 соответственно. Это можно доказать, представив число в виде суммы, где последняя цифра определяет делимость всего числа.

Примеры

1. 100: Оканчивается на 0, делится на 10, 5 и 2.
2. 12687: Оканчивается на 7, не делится на 2, 5 и 10.
3. 12340: Оканчивается на 0, делится на 10, 5 и 2.
4. 456: Оканчивается на 6, делится на 2, но не на 5 и 10.
5. 720: Оканчивается на 0, делится на 10, 5 и 2.

Заключение

Важно отметить, что по последней цифре можно судить только о делимости на 2, 5 и 10. Для других чисел этот признак не работает.

Список рекомендованной литературы

1. Виленкин Н.Я. и др. «Математика. 6 класс». М.: Мнемозина, 2013.
2. Зубарева И.И., Мордкович А.Г. «Математика. 6 класс». М.: Мнемозина.
3. Истомина И.Б. «Математика, 6 класс». М.: Ассоциация ХХI век.

Дополнительные ресурсы

• Интернет-портал «onlinemschool.com»

Домашнее задание

1. Изучить страницы 9-10 учебника Виленкина, выполнить задания на страницах 10 № 32 и 11 № 36.
2. Назовите признаки делимости чисел на 2, 5 и 10.
3. Укажите среди следующих чисел те, что делятся на 2, 5 и 10:
   • а) 13
   • б) 100
   • в) 129
   • г) 130
   • д) 720
   • е) 12398050
   • ж) 945
   • з) 53846030

Ответьте на вопросы:

1. Какое наименьшее пятизначное число кратно пяти?
2. Какое наибольшее трёхзначное число кратно двум?
3. Укажите семь чисел, которые делятся на десять.