Чем старше дерево, тем оно выше. Чем медленнее темп, тем дольше идти до школы. Эти и другие процессы можно описать в математических терминах, в виде прямой пропорциональной зависимости или обратной пропорциональной зависимости. О том, как это делается, мы расскажем в этой статье.

Прямая пропорциональность представляет собой зависимость, при которой увеличение или уменьшение одной величины приводит к аналогичному изменению другой величины в том же соотношении.

Пример:
Время работы и заработная плата при фиксированной почасовой ставке.

Формула:
y = kx, где k — коэффициент пропорциональности.

Основные определения

Математическая зависимость — это связь между элементами двух множеств, при которой каждому элементу одного множества соответствует элемент из другого множества.

Виды зависимостей:

• Прямая зависимость. С увеличением одной величины увеличивается и вторая; с уменьшением одной величины уменьшается и вторая.
• Обратная зависимость. С увеличением одной величины вторая уменьшается; с уменьшением одной величины вторая увеличивается.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Две величины считаются пропорциональными, если их отношение остается постоянным.

Пропорциональность — это связь между двумя величинами, при которой изменение одной из них вызывает изменение другой в том же масштабе. Проще говоря, это зависимость одного числа от другого.

Существует два типа пропорциональности:

1. Прямая пропорциональность. Увеличение одной величины ведет к аналогичному увеличению другой; уменьшение одной величины приводит к уменьшению другой.

2. Обратная пропорциональность. Уменьшение одной величины вызывает увеличение другой, и наоборот — увеличение одной величины приводит к уменьшению другой.

Коэффициент пропорциональности — это постоянное соотношение между пропорциональными величинами. Он показывает, сколько единиц одной величины соответствует одной единице другой. Этот коэффициент обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины считаются прямо пропорциональными, если при увеличении или уменьшении одной из них в несколько раз другая величина изменяется аналогично.

Прямая пропорциональность может быть представлена в виде схемы: «больше — больше» или «меньше — меньше».

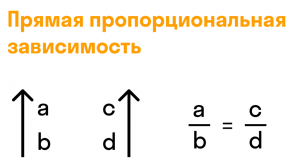
a и d называются крайними членами пропорции, в то время как b и c являются средними членами.

Основное свойство пропорции

Произведение крайних членов равно произведению средних членов.

Свойство прямо пропорциональной зависимости

Если две величины находятся в прямой пропорциональности, то отношения их соответствующих значений равны.

Примеры прямо пропорциональной зависимости:

• При постоянной скорости расстояние, пройденное за определенное время, прямо пропорционально времени.
• Периметр квадрата и длина его стороны — прямо пропорциональные величины.
• Стоимость конфет, купленных по фиксированной цене, прямо пропорциональна количеству.

Чтобы проиллюстрировать разницу между прямой и обратной пропорциональностью, можно использовать метафору: «Чем дальше в лес, тем больше дров». Это означает, что чем больше времени ты проводишь в лесу, тем больше дров ты сможешь собрать.

Формула прямой пропорциональности

y = kx, где y и x — переменные величины, а k — постоянная величина, известная как коэффициент прямой пропорциональности.

Коэффициент прямой пропорциональности представляет собой отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула для коэффициента прямой пропорциональности:
yx=kxy​=k

Пример 1

Два автомобиля отправились в одно и то же путешествие. Один из них двигался со скоростью 70 км/ч и за 2 часа проехал тот же путь, что и другой автомобиль за 7 часов. Найдите скорость второго автомобиля.

Решение:
Используем формулу для расчета пути через скорость и время:
$S=V\cdot t$

Так как оба автомобиля проехали одинаковое расстояние, можем составить пропорцию:

$70\cdot 2=V\cdot 7$

Теперь найдем скорость второго автомобиля:

V=70⋅27=20V=770⋅2​=20

Ответ: 20 км/ч.

Пример 2

Блогер может написать 14 постов за 8 дней. Сколько помощников ему потребуется, чтобы написать 420 постов за 12 дней, если они работают с той же скоростью?

Решение:
Количество людей (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно выполнить за одно и то же время.

Составим пропорцию:

14 постов8 дней×x (блогеров)=420 постов12 дней8 дней14 постов​×x (блогеров)=12 дней420 постов​

Согласно основному свойству пропорции:

$14x\cdot 12=420\cdot 8$

Решим уравнение для x:

x=420⋅814⋅12=20x=14⋅12420⋅8​=20

Ответ: 20 человек смогут написать 420 постов за 12 дней.

Обратно пропорциональные величины

Когда одна из двух величин увеличивается (или уменьшается) в несколько раз, другая уменьшается (или увеличивается) на то же число, это называется обратной пропорцией. Объясните смысл обратной пропорции с помощью диаграммы: «больше — меньше» и «меньше — больше». 

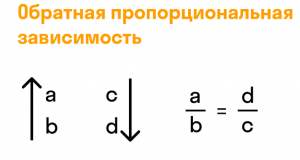
Свойство обратной пропорциональности величин

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно выбранных значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

• Время, необходимое для преодоления определенного маршрута, и скорость, с которой этот маршрут был пройден, являются обратно пропорциональными величинами.
• При одинаковой продуктивности количество школьников, работающих над одной задачей, обратно пропорционально времени, необходимому для её решения.
• Количество конфет, которые можно купить на фиксированную сумму денег, обратно пропорционально их цене.

Формула обратной пропорциональности

y=kxy=xk​

где y и x — переменные величины, а k — постоянная величина, называемая коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности представляет собой произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула для коэффициента обратной пропорциональности:
$xy=k$

Пример для практики

Задача 1: 24 человека смогли раскрутить канал на YouTube за 5 дней. Сколько дней потребуется 30 людям для выполнения той же работы, если они будут работать с такой же эффективностью?

Решение:

В этом случае, чем больше людей участвует в работе, тем меньше времени потребуется для её выполнения. Это указывает на обратно пропорциональную зависимость.

Таким образом, направление стрелки будет от большего числа людей к меньшему времени. Обратная пропорция может быть представлена следующим образом:

$24\text{ человека}\times 5\text{ дней}=30\text{ человек}\times x\text{ дней}$

Теперь решим уравнение:

$24\times 5=30\times x$

$120=30x$

x=12030=4x=30120​=4

Ответ: 30 человек смогут выполнить ту же работу за 4 дня.

Пример 1.

Предположим, что 30 человек могут раскрутить канал за $x$ дней. Составим пропорцию:

Чтобы найти неизвестный член пропорции, нужно умножить средние члены и разделить на известный крайний член:

Вычисляем:

Таким образом, 30 человек смогут раскрутить канал за 4 дня.

Ответ: 4 дня.

Пример 2.

Автомобиль проезжает расстояние между двумя городами за 13 часов при скорости 75 км/ч. Необходимо узнать, сколько времени потребуется, если скорость составит 52 км/ч.

Рассуждение:

Скорость и время имеют обратно пропорциональную зависимость: чем выше скорость, тем меньше времени потребуется для преодоления одного и того же расстояния.

Обозначим:

• v1=75v1​=75 км/ч (первая скорость)
• v2=52v2​=52 км/ч (вторая скорость)
• t1=13t1​=13 ч (время при первой скорости)
• t2=xt2​=x (неизвестное время при второй скорости)

Решение:

Составим пропорцию:

Это означает, что соотношения равны, но обернуты.

Подставим известные значения:

Теперь выразим t2t2​:

Вычисляем:

Разделим 18.75 на целую и дробную части:

18 часов 0.75 часа — это 45 минут.

Ответ: 18 часов 45 минут.