Введение

Если вы столкнётесь с трудностями в понимании материала, рекомендуем обратиться к уроку «Упрощение выражений».

Как раскрыть скобки, когда впереди стоит знак «+»

Применение сочетательного закона сложения. Когда нужно прибавить сумму двух чисел к какому-то числу, можно сначала прибавить одно слагаемое, а затем и другое.

На левой стороне уравнения будет выражение со скобками, тогда как на правой — без них. Это означает, что при переходе от левой части уравнения к правой мы осуществляем раскрытие скобок.

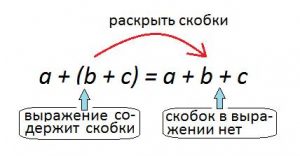
Пример 1.

48 + (12 + 14)

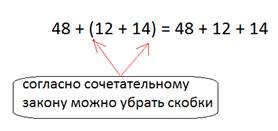
При раскрытии скобок мы меняем порядок операций, облегчая вычисления.

Пример 2. 

48 + (12 — 14)

Пример 3.

48 + (- 12 + 14)

Во всех трех примерах мы всего лишь убираем скобки, формируя правило:

Если перед скобками стоит «плюс»,
то скобки и этот знак «плюс» можно убрать,
а знаки перед числами внутри скобок
останутся без изменений.

Обрати внимание:

Если первое слагаемое внутри скобок не имеет знака, нужно воспринимать его со знаком «плюс».

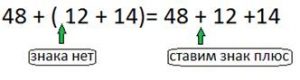
Пример 1.

111 + (889 + 445)

Рассмотрим выполнение по шагам. Сначала к 889 прибавляется 445. Выполнить это в уме можно, однако это не всегда просто. Упростив порядок действий, мы сможем ускорить вычисления.

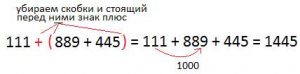
Пример 2.

1345 + (- 345 + 512)

По заданному порядку действий сначала надо из 512 вычесть 345, а потом добавить 1345 к результату. Раскрыв скобки, мы изменяем порядок вычислений и тем самым упрощаем процесс.

Раскрытие скобок с предшествующим знаком «−»

На примере объясним правило: для нахождения значения выражения, сложим 2 и 5, после чего применим к результату обратный знак, получив -7.

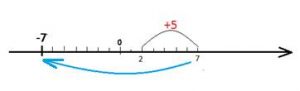
С другой стороны, такой же результат можно достичь сложением чисел, противоположных первоначальным.

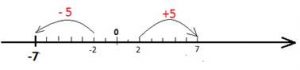
Формулировка правила:

Если перед скобками стоит знак «минус», то скобки и этот знак «минус» можно убрать, а знаки перед числами внутри скобок изменить на противоположные. 

a — (b + c) = a — b — c ; a — (b — c) = a — b + c

Пример 1. 

17 — (13 — 4)

Это правило остаётся неизменным, даже если в скобках содержится три или более слагаемых.

Пример 2.

16 — (12 — 3 + 1)

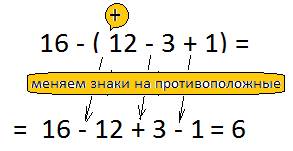
Примечание: Знаки изменяются на противоположные только у слагаемых.

Пример 3.

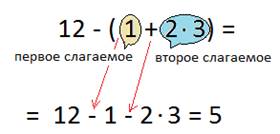
12 — (1 + 2 · 3)

Примеры с буквенными выражениями

Пример 1.

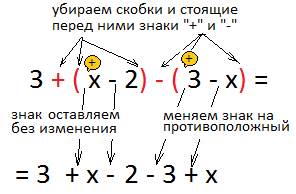
3 + (x — 2) — (3 — x)

Пример 2.

1 + 2 · (x — 1) — 3 · (x — 2)

Чтобы раскрыть скобки, необходимо вспомнить распределительное свойство.

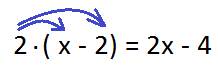
Сначала умножаем первую скобку на 2, вторую — на 3.

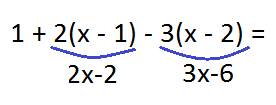
Если перед первой скобкой стоит знак «+», знаки остаются прежними. Если перед второй скобкой «−», все знаки меняются на противоположные.

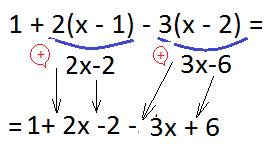
Заключение

В списке литературы приведены учебные издания, которые помогут закрепить материал и уточнить прогресс:

• Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6. – М.: Мнемозина, 2012.
• Мерзляк А. Г., Полонский В. В., Якир М.С. Математика 6 класс. – Гимназия, 2006.
• Депман И. Я., Виленкин Н. Я. За страницами учебника математики. – Просвещение, 1989.
• Рурукин А. Н., Чайковский И. В. Задания по курсу математика 5-6 класс – ЗШ МИФИ, 2011.
• Рурукин А. Н., Сочилов С. В., Чайковский К. Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
• Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.