Введение

Предпочтение зачастую отдается восприятию информации через визуальные изображения, а не через числовые данные. Для этого нередко используются графические способы представления данных, такие как диаграммы и графики. В пятом классе нас уже познакомили с одним из типов диаграмм — круговыми диаграммами.

Круговая диаграмма

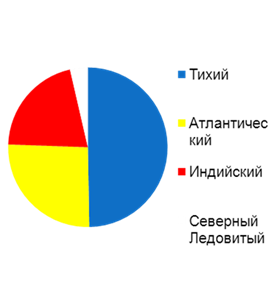
Рис. 1. Круговая диаграмма распределения площадей океанов в общей площади мирового океана.

Из этого изображения видно, что Тихоокеанский океан не только самый крупный, но и занимает почти половину всей водной поверхности Земли.

Рассмотрим еще один пример.

Четыре планеты, наиболее приближенные к нашему светилу, известны как планеты земной группы.

Ниже приведены расстояния от Солнца до каждой из планет:

• Меркурий: 58 млн км
• Венера: 108 млн км
• Земля: 150 млн км
• Марс: 228 млн км

Мы снова можем воспользоваться круговой диаграммой, чтобы показать, как каждое расстояние вносит свой вклад в общую сумму расстояний. Однако совокупность всех расстояний не имеет практического значения. Полная окружность не передает никакой значимой величины (см. Рис. 2).

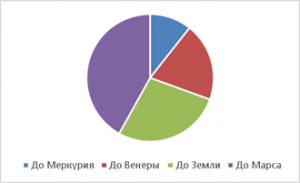
Рис. 2 Круговая диаграмма расстояний до Солнца.

Исходя из отсутствия значимого смысла в сумме данных величин, необходимость в построении круговой диаграммы пропадает.

Столбчатая диаграмма

Однако мы можем успешно отобразить все расстояния с помощью элементарных геометрических фигур — прямоугольников или столбиков. Каждому числовому значению будет соответствовать свой столбик. Чем больше величина, тем выше соответствующий ей столбик. Сумма величин нам не нужна.

Чтобы наглядно отображать высоту каждого столбика, создаем декартову систему координат и размечаем вертикальную ось по миллионам километров.

Строим четыре столбика, отображающие расстояния от Солнца до соответствующих планет (см. Рис. 3).

• Меркурий: 58 млн км
• Венера: 108 млн км
• Земля: 150 млн км
• Марс: 228 млн км

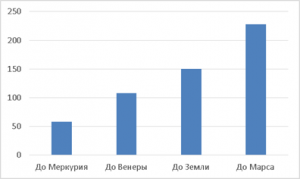
Рис. 3. Столбчатая диаграмма расстояний до Солнца.

Сравним различные типы диаграмм (см. Рис. 4).

Столбчатая диаграмма оказывается более информативной:

1. Она наглядно показывает наименьшее и наибольшее расстояния.
2. Видно, что каждое последующее расстояние возрастает примерно на 50 млн км.

Соображения по выбору диаграмм

Если стоит задача построить диаграмму — круговую или столбчатую — важно решить:

• Требуется ли вам сумма всех величин и есть ли она смысл?
• Хотите ли вы видеть вклад каждой величины в общую сумму?

Если ответ утвердительный, целесообразно строить круговую диаграмму; если ответ отрицательный — выбирайте столбчатую.

Пример, когда круговая диаграмма имеет смысл, это площади океанов: их сумма представляет собой общую площадь мирового океана. С другой стороны, сумма расстояний до различных планет значимого смысла не несет. В этом случае столбчатая диаграмма более полезна.

Задача 1

Построить диаграмму температурных изменений для каждого месяца года.

Температура передана в Таблице 1:

• Январь: -18
• Февраль: -11
• Март: 2
• Апрель: 7
• Май: 14
• Июнь: 20
• Июль: 21
• Август: 18
• Сентябрь: 15
• Октябрь: 9
• Ноябрь: 6
• Декабрь: -8

Табл. 1

Суммарное значение температур для нас не столь значимо. (Значение появляется, если мы разделим его на 12, чтобы получить среднегодовую температуру, но это не тематика нашего урока.)

Следовательно, мы будем строить столбчатую диаграмму.

Минимальное значение — -18, максимальное — 21.

Таким образом, на вертикальной оси будет достаточно значений от -20 до +25.

Изобразим 12 столбиков для каждого месяца.

Столбики, отображающие отрицательные температуры, направлены вниз (см. Рис. 5).

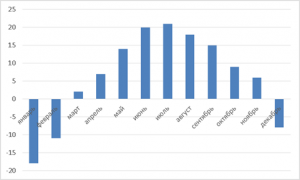
Рис. 5. Столбчатая диаграмма температурных изменений за каждый месяц в течение года.

Что демонстрирует диаграмма?

Просто определить месяц с самой низкой и самой высокой температурой. Видно конкретное значение для каждого месяца и очевидно, что летние месяцы менее разнятся между собой, в отличие от осенних или весенних.

Таким образом, чтобы построить столбчатую диаграмму, следует:

1. Начертить координатные оси.
2. Определить минимальное и максимальное значения и сделать соответствующую разметку вертикальной оси.
3. Построить столбики для каждой величины.

Рассмотрим возможные трудности при построении.

Пример 1

Построить столбчатую диаграмму расстояний от Солнца до ближайших 4 планет, а также до ближайшей звезды.

Мы уже знаем о планетах, а ближайшая звезда — Проксима Центавра (см. Табл. 2).

• Меркурий: 58
• Венера: 108
• Земля: 150
• Марс: 228
• Проксима Центавра: 40 000 000

Табл. 2

Расстояния указаны в миллионах километров.

Создаем столбчатую диаграмму (см. Рис. 6).

Рис. 6. Столбчатая диаграмма расстояния от солнца до планет земной группы и ближайшей звезды.

Однако расстояние до звезды настолько велико, что по сравнению с ним расстояния до четырех планет становятся неразличимыми.

Диаграмма теряет всякий смысл.

Заключение: невозможно строить диаграмму, основываясь на данных, которые значительно варьируются друг от друга.

Как с этим справиться?

Следует разбивать данные на группы. Строим одну диаграмму для планет, как делали ранее, и другую — для звезд.

Пример 2

Построить столбчатую диаграмму для температур плавления металлов (см. Табл. 3).

• Медь: 1083
• Серебро: 960
• Золото: 1063

Табл. 3. Температуры плавления металлов.

При построении диаграммы мы почти не замечаем разницу между медью и золотом (см. Рис. 7).

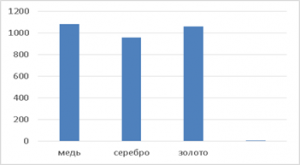
Рис. 7. Столбчатая диаграмма температур плавления металлов (градировка с 0 градусов).

У всех трех металлов высокая температура плавления. Область диаграммы ниже 900 градусов нам неактуальна. Поэтому лучше ее не отображать.

Начнем градировку с 880 градусов (см. Рис. 8).

Рис. 8. Столбчатая диаграмма температур плавления металлов (градуировка с 880 градусов).

Это позволяет нам более точно изобразить столбики.

Теперь четко видны температуры и их соотношения. Сравнения между величинами более наглядны, когда нижние части столбиков удалены, и отображаются только верхушки при увеличении.

Если все значения начинаются с достаточно высокого уровня, то градуировку можно начать с этого уровня, а не с нуля, для улучшения наглядности диаграммы.

Электронные таблицы

Ручное создание диаграмм — это длительный и сложный процесс. Сегодня для быстрой и красивой генерации диаграмм любого типа часто применяются электронные таблицы, такие как Excel или аналогичные приложения, например Google Docs.

Достаточно внести данные, и программа сама построит необходимую диаграмму.

Построим диаграмму, показывающую количество людей, для которых определенный язык является родным.

Данные взяты из Википедии. Заносим их в таблицу Excel (см. Табл. 4).

• Английский: 500
• Арабский: 300
• Испанский: 425
• Китайский: 1200
• Немецкий: 120
• Португальский: 230
• Русский: 160
• Французский: 75

Табл. 4

Выделяем данные таблицы и изучаем предлагаемые типы диаграмм.

Наличие как круговых, так и столбчатых диаграмм предлагает возможность построить обе.

Круговая (см. Рис. 9):

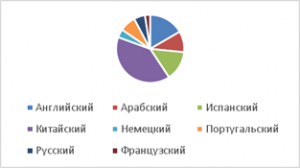
Рис. 9. Круговая диаграмма долей языков.

Столбчатая (см. Рис. 10):

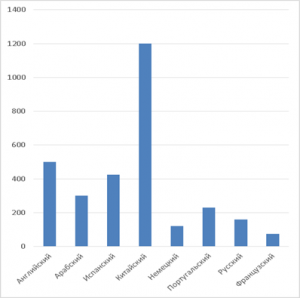
Рис. 10. Столбчатая диаграмма, иллюстрирующая количество людей с данным родным языком.

В каждом случае при выборе диаграммы необходимо решить, какой тип более подходит. Заготовленную диаграмму можно легко скопировать и вставить в любой документ.

Как видите, создание диаграмм сегодня вовсе не является сложной задачей.

Применение диаграмм в реальной жизни

Рассмотрим применение диаграмм в реальных ситуациях. Вот, например, информация по количеству уроков по основным дисциплинам в шестом классе (см. Табл. 5).

Учебные дисциплины

• Количество уроков в неделю
• Количество уроков за год
• Русский язык: 6, 210
• Литература: 2, 70
• Английский язык: 3, 105
• Математика: 5, 175
• История: 2, 70
• Обществознание: 1, 35
• География: 1, 35
• Биология: 2, 70
• Музыка: 1, 35

Табл. 5

Представленные данные не очень удобны для анализа. Следующая диаграмма (см. Рис. 11) показывает информацию визуально.

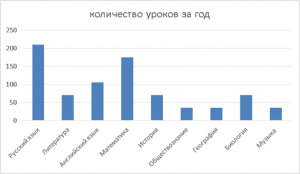
Рис. 11. Количество уроков за год.

Теперь облегчить сравнение позволила сортировка данных по убыванию (см. Рис. 12).

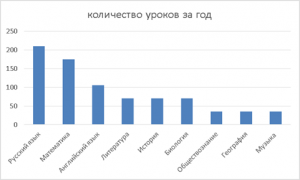
Рис. 12. Количество уроков за год (по убыванию).

Эта диаграмма позволяет легко определить, каких уроков больше всего и каких меньше. Также видно, что занятий по английскому в два раза меньше, чем по русскому, что логично на фоне повседневного использования последнего как родного языка.

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.