Главная > Свойства диагоналей прямоугольника
Свойства диагоналей прямоугольника
Введение: Четырехугольники и их элементы
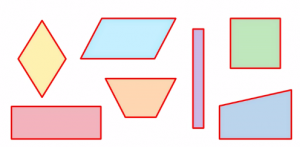
Рассмотрим геометрические фигуры, изображенные на рисунке 1. Все эти фигуры имеют по четыре стороны, что делает их многоугольниками, а именно четырехугольниками.

Элементы четырехугольников
Каждая из фигур на рисунке 1 обладает следующими характеристиками:
- Стороны: Все фигуры имеют по четыре стороны (рис. 2).
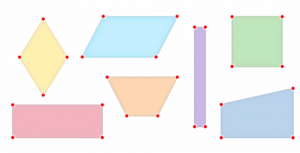
- Вершины: У всех фигур по четыре вершины (рис. 3).
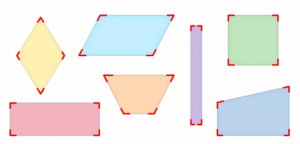
- Углы: Каждая фигура содержит по четыре угла (рис. 4).
Прямоугольники
Теперь разделим фигуры на две группы. В первую группу входят четырехугольники, у которых все углы являются прямыми (рис. 5). Эти четырехугольники называются прямоугольными четырехугольниками или просто прямоугольниками.

Свойства прямоугольника
Рассмотрим более подробно прямоугольник (рис. 6). У него все углы прямые, что можно проверить с помощью прямоугольного треугольника (рис. 7).


Чтобы убедиться, что углы прямые, приложим прямой угол прямоугольного треугольника к углу прямоугольника (рис. 8).

Если стороны и вершины совпадают, значит, угол действительно прямой. Проверяем каждый угол аналогичным образом (рис. 9, 10, 11).



Противоположные стороны прямоугольника равны (рис. 12). Например, стороны AB и CD – это противоположные стороны.

Также стороны AD и BC равны (рис. 13).

Диагонали прямоугольника и их свойства
Отрезки AC и BD (рис. 14) называются диагоналями прямоугольника. Чтобы сравнить их длину, воспользуемся циркулем (рис. 15).
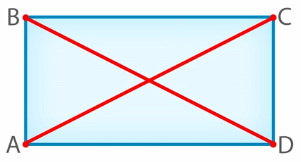
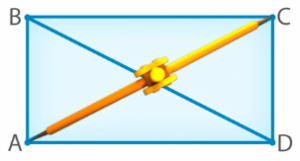
Для этого поставим одну ножку циркуля на точку A, а вторую – на точку C (рис. 16). Не изменяя расстояния между ножками, перенесем циркуль на отрезок BD (рис. 17). Если ножки совпадают с точками B и D, значит, диагонали равны.
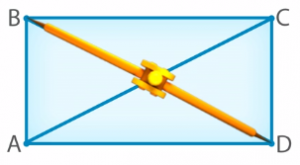
Точка пересечения диагоналей
Точка O – это точка пересечения диагоналей AC и BD (рис. 18). Теперь сравним отрезки AO, OC, BO и OD. Снова воспользуемся циркулем. Убедившись, что AO равно OC (рис. 19 и 20), мы видим, что отрезки, образованные пересечением диагоналей, равны.
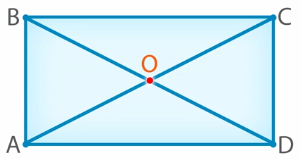
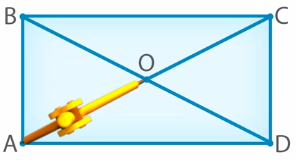
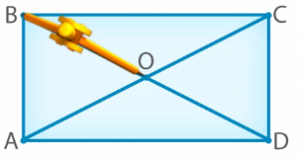
Аналогично проверим отрезки BO и OD, используя циркуль (рис. 21 и 22). Мы видим, что они также равны.
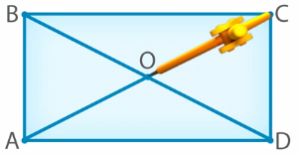
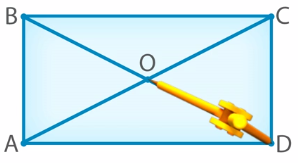
Заключение
Попробуйте самостоятельно начертить любой прямоугольник и проверить два вывода:
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей делит их на равные отрезки.
Список литературы
- Петерсон Л. Г. Математика. 4 класс. Учебник в 3 ч. – М.: 2013. – 96 с. + 128 с. + 96 с.
- Математика. Учебник для 4 кл. нач. шк. В 2 ч. / М. И. Моро, М. А. Бантова – М.: Просвещение, 2010.
- Математика. 4 класс. Учебник в 2 ч. Башмаков М. И., Нефедова М. Г. – 2009. – 128 с., 144 с.
Дополнительные ресурсы
- Интернет-портал «myshared.ru»
- Интернет-портал «myshared.ru»
Домашнее задание
Ответьте на следующие вопросы:
- Сколько диагоналей у прямоугольника?
- Верно ли утверждение, что все четырехугольники являются прямоугольниками?
- Какие элементы вы знаете у прямоугольников?
- Что такое диагональ?
Оцените урок:




