Треугольник и его составляющие

Треугольник – это геометрическая фигура, образованная тремя точками, которые не находятся на одной прямой, и тремя отрезками, соединяющими эти точки. В каждом треугольнике выделяют следующие элементы:

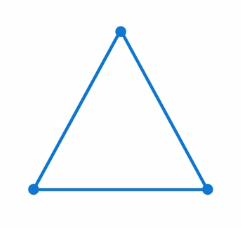
Вершины (см. рис. 1). Это точки, в которых сходятся стороны треугольника. 

Стороны (см. рис. 2). Это отрезки, соединяющие вершины. 

Углы (см. рис. 3). Это углы, образованные двумя сторонами треугольника.

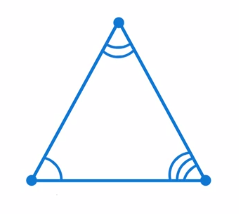
Виды углов

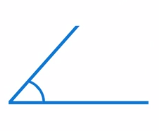
Развернутый угол (см. рис. 4). Угол, у которого стороны лежат на одной прямой.

Прямой угол (см. рис. 5). Это угол, который составляет половину развернутого угла.

Для наглядной проверки прямого угла можно использовать модель, сложив лист бумаги дважды (см. рис. 6 и 7). Сравнив модель с углом на чертеже, мы можем убедиться в его прямом угле.

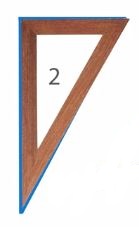
Для облегчения определения прямого угла применяется специальный инструмент – прямоугольный треугольник (см. рис. 8).

Углы, которые не являются прямыми, делятся на острые (см. рис. 9) и тупые (см. рис. 11).

• Острый угол меньше прямого (см. рис. 10).

• Тупой угол больше прямого (см. рис. 12).

Виды треугольников

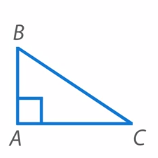
• Прямоугольный треугольник (см. рис. 13). Один из углов этого треугольника является прямым.

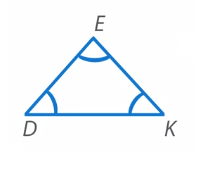
• Остроугольный треугольник (см. рис. 14). Все углы в таком треугольнике острые.

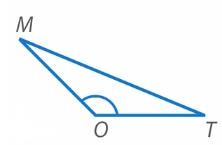
• Тупоугольный треугольник (см. рис. 15). У него есть один тупой угол.

Задание 1 (определение вида треугольников)

Назовите номера треугольников, которые являются тупоугольными, остроугольными и прямоугольными на рисунке 16.

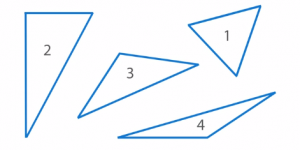
• Треугольник номер 1 – остроугольный, так как все его углы острые.
• Треугольники номер 3 и 4 – тупоугольные, у каждого из них есть один тупой угол.
• Треугольник номер 2 – прямоугольный. Мы можем проверить его прямой угол с помощью прямоугольного треугольника (см. рис. 17).

Задание 2 (построение прямоугольного треугольника)

Постройте на нелинованной бумаге треугольник, в котором угол будет прямым, длина одной стороны составит 15 см, а другой – 20 см.

Начнем с точки A (см. рис. 18).

Проведем через точку A прямую (см. рис. 19).

Для построения прямого угла воспользуемся прямоугольным треугольником, приложив его так, чтобы вершина прямого угла совпала с точкой A (см. рис. 20).

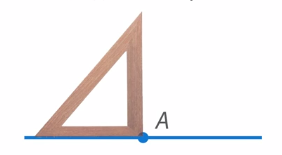
Проведем луч из точки A по второй стороне треугольника, чтобы получить прямой угол (см. рис. 21).

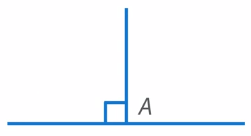
Теперь построим отрезок AB длиной 15 см (см. рис. 22).

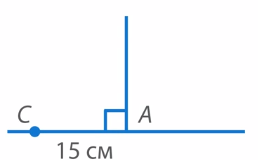Затем построим отрезок AC длиной 20 см (см. рис. 23).

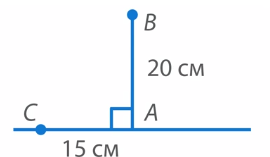
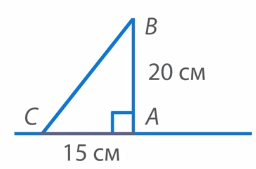
Соединим точки B и C отрезком (см. рис. 24). Мы получили прямоугольный треугольник ABC с прямым углом A и сторонами AB = 15 см и AC = 20 см.

Виды треугольников по длине сторон

В зависимости от длины сторон треугольники делятся на разносторонние и равнобедренные. Если длины всех сторон треугольника различны, то он называется разносторонним. Если две стороны равны, такой треугольник называется равнобедренным, причем равные стороны называют боковыми, а третью сторону – основанием.

Задание 3 (построение прямоугольного равнобедренного треугольника и прямоугольника)

Постройте равнобедренный треугольник ABC с прямым углом A и сторонами AB и AC по 20 см. Затем дополните его до прямоугольника.

Начнем с точки A (см. рис. 25).

Проведем через точку A прямую (см. рис. 26).

Для построения прямого угла воспользуемся прямоугольным треугольником, приложив его так, чтобы вершина прямого угла совпала с точкой A (см. рис. 27).

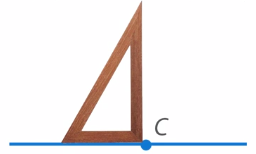
Проведем луч из точки A по второй стороне треугольника (см. рис. 28).

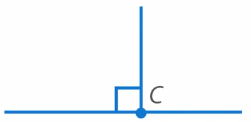
Теперь отложим на каждом луче отрезок длиной 20 см, обозначив их буквами B и C (см. рис. 29).

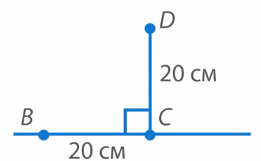
Соединим точки B и C отрезком (см. рис. 30). Мы получили прямоугольный треугольник ABC с прямым углом A и сторонами AB и AC по 20 см.

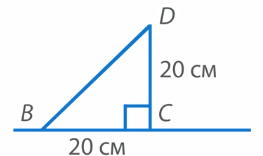
Теперь достроим треугольник до прямоугольника. Для этого построим прямой угол с вершиной D, приложив прямоугольный треугольник так, чтобы его вершина совпала с точкой C (см. рис. 31).

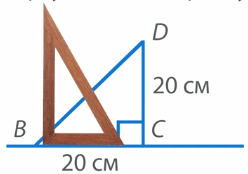
1. Проведем луч из точки C по второй стороне треугольника (см. рис. 32).
2. Отложим отрезок от точки D, равный 20 см (см. рис. 33).
3. Соединим точки D и B отрезком (см. рис. 34). Мы получили прямоугольник ABCD.
4. Обратите внимание, что если все стороны равны, то получился квадрат (см. рис. 35).

Заключение

Сегодня мы познакомились с различными видами треугольников: остроугольными, тупоугольными и прямоугольными, а также научились строить прямоугольный треугольник на нелинованной бумаге с помощью инструмента «прямоугольный треугольник».

Список литературы

1. Петерсон Л. Г. Математика. 4 класс. Учебник в 3 ч. – М.: 2013. – 96 с. + 128 с. + 96 с.
2. Демидова Т. Е., Козлова С. А., Тонких А. П. Математика. 4 класс. Учебник в 3 ч. 2-е изд., испр. – М.: 2013.; Ч. 1 – 96 с., Ч. 2 – 96 с., Ч. 3 – 96 с.
3. Математика. Учебник для 4 кл. нач. шк. В 2 ч. / М. И. Моро, М. А. Бантова – М.: Просвещение, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «interneturok.ru» (Источник)
2. Интернет-портал «festival.1september.ru» (Источник)
3. Интернет-портал «myshared.ru» (Источник)

Домашнее задание

1. Постройте на нелинованной бумаге прямоугольный треугольник  со сторонами  см и  см. Какой вид имеет такой треугольник?

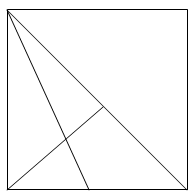
2.Сколько на рисунке треугольников? Сколько из них прямоугольных?

3.Задача на смекалку.

Нильс летел в своей стае на спине гуся Мартина. Он обратил внимание, что построение стаи напоминает треугольник: впереди вожак, затем два гуся, в третьем ряду три и т. д. Стая остановилась на ночлег на льдине. Нильс увидел, что расположение гусей на этот раз напоминает квадрат, состоящий из рядов, в каждом ряду – одинаковое количество гусей, причем число гусей в каждом ряду равно числу рядов. Гусей в стае меньше 50. Сколько гусей в стае?