Повторение названий и свойств геометрических фигур

Сегодня мы отправимся в страну Геометрия, где изучим различные виды треугольников.

Посмотрите на геометрические фигуры и определите, какая из них является «лишней» (см. рис. 1).

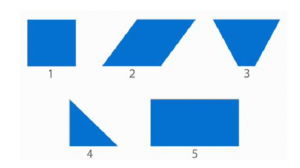
Рис. 1. Иллюстрация к примеру

Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).

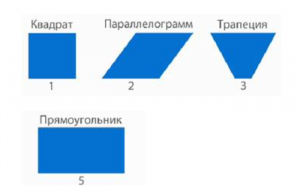
Рис. 2. Четырехугольники

Значит, «лишней» фигурой является треугольник (рис. 3).

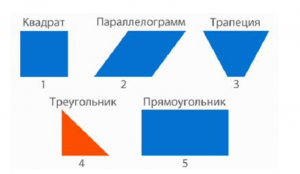
Рис. 3. Иллюстрация к примеру

Треугольник представляет собой фигуру, состоящую из трех точек, которые не располагаются на одной прямой, и трех отрезков, соединяющих эти точки попарно.

Эти точки именуются вершинами треугольника, а отрезки – его сторонами. Стороны треугольника формируют три угла, расположенные в его вершинах.

Изучение основных свойств треугольника

Главными характеристиками треугольника являются три стороны и три угла. В зависимости от величины углов, треугольники делятся на остроугольные, прямоугольные и тупоугольные.

Классификация треугольников по величине угла

Треугольник называется остроугольным, если все его углы острые, то есть каждый из них меньше 90° (см. рис. 4).

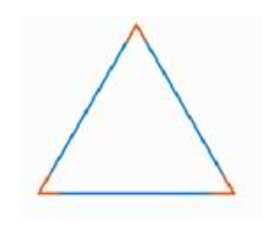
Рис. 4. Остроугольный треугольник

Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).   

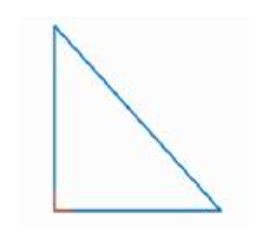
Рис. 5. Прямоугольный треугольник

Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).

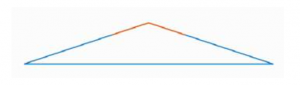
Рис. 6. Тупоугольный треугольник

Знакомство с видами по числу равных сторон

По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.

Равнобедренным называется треугольник, у которого две стороны равны (рис. 7). 

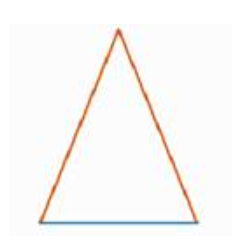
Рис. 7. Равнобедренный треугольник

Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.

Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).

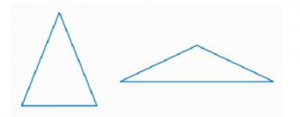
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники 

Равносторонним называется треугольник, у которого все три стороны равны (рис. 9). 

Рис. 9. Равносторонний треугольник

В равностороннем треугольнике все углы равны. Равносторонние треугольники всегда остроугольные.

Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10). 

Рис. 10. Разносторонний треугольник

Выполнение тренировочных упражнений, деление на группы

Выполните задание. Распределите данные треугольники на три группы (рис. 11).

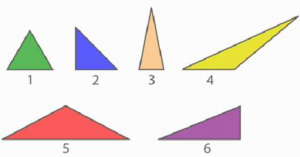
Рис. 11. Иллюстрация к заданию

Сначала классифицируем треугольники по величине углов.

Остроугольные треугольники: № 1, № 3.

Прямоугольные треугольники: № 2, № 6.

Тупоугольные треугольники: № 4, № 5.

Затем распределим те же треугольники на группы по числу равных сторон.

Разносторонние треугольники: № 4, № 6.

Равнобедренные треугольники: № 2, № 3, № 5.

Равносторонний треугольник: № 1.

Решение геометрической задачи

Исследуйте рисунки треугольников.

Подумайте, какой длины кусок проволоки был использован для создания каждого треугольника (рис. 12). И еще: какие свойства треугольников помогут вам определить, из какого куска проволоки был сделан каждый из них?

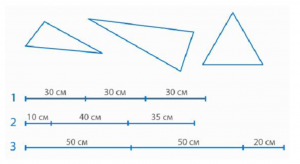
Рис. 12. Иллюстрация к заданию

Можно рассуждать следующим образом.

Первый кусок проволоки разделен на три равные части, что позволяет создать равносторонний треугольник. Он изображен на рисунке под номером три.

Второй кусок проволоки состоит из трех разных по длине частей, поэтому из него можно сформировать разносторонний треугольник. На рисунке он обозначен первым.

Третий кусок проволоки состоит из трех частей, две из которых имеют одинаковую длину, что позволяет сделать равнобедренный треугольник. Он представлен на рисунке под номером два.

Сегодня на уроке мы познакомились с различными типами треугольников.

Список литературы

1. М. И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М. И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М. И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. Школа России: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С. И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В. Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Домашнее задание

Подготовьте короткое изложение о различных типах треугольников и их свойствах.

1. Закончите фразы.

а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.

б) Точки называются …, отрезки – его …. Стороны треугольника образуют в вершинах треугольника ….

в) По величине угла треугольники бывают … , … , … .

г) По числу равных сторон треугольники бывают … , … , … .

2. Начертите

а) прямоугольный треугольник;

б) остроугольный треугольник;

в) тупоугольный треугольник;

г) равносторонний треугольник;

д) разносторонний треугольник;

е) равнобедренный треугольник.

3. Составьте задание по теме урока для своих товарищей.