Ведение:

Этот урок посвящен исследованию координатной плоскости. Мы изучим, какую роль играют координатные плоскости, и рассмотрим основные принципы. В ходе занятия мы узнаем, как преобразовать обычную плоскость в координатную и решим примеры, в которых будем учиться наносить точки по заданным координатам и определять координаты точек, найденных на координатной плоскости.

Основные сведения о координатной плоскости
Каждый дом имеет определенный номер и название улицы — это аналог его адреса. На билете в зрительный зал указаны номер ряда и место — это адрес стула. Для определения позиции на глобусе используются долгота и широта, являющиеся адресом географической точки (географические координаты). Каждому объекту сопоставляется определенный адрес в виде координат. Таким образом, адрес или координаты — это числовая или буквенная метка, позволяющая определить местоположение объекта.

Математики разработали модель, которая, в частности, позволяет описывать любую аудиторию (распределение мест). Эта модель называется координатной плоскостью.

Чтобы преобразовать обыкновенную плоскость в координатную, необходимо изобразить две взаимно перпендикулярные линии, указывая стрелками направления «вправо» и «вверх» (см. Рис. 1). На линиях делают отметки, как на линейке, и точка их пересечения является нулевой точкой для обеих осей. Горизонтальная линия называется осью абсцисс, вертикальная — осью ординат.

Две взаимоперпендикулярные оси с отметками называют прямоугольной либо декартовой системой координат. Название «декартова» связано с именем французского философа и математика Рене Декарта, предложившего данную систему.

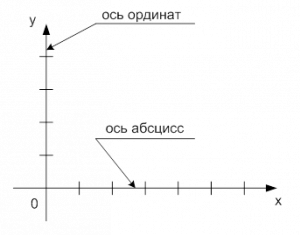
Рис. 1. Координатная плоскость

Координаты точек
Для любой точки на координатной плоскости можно определить пару чисел (координат). На рисунке 2 представлена точка на координатной плоскости. Для нахождения координат этой точки необходимо через точку провести две линии, параллельные координатным осям (пунктирной линией). Пересечение одной линии с осью абсцисс дает координату точки, а пересечение другой линии с осью ординат — координату . Сначала пишут координату , затем . Точка имеет координаты . Аналогично, находим координаты точки , она имеет координаты (см. Рис. 2).

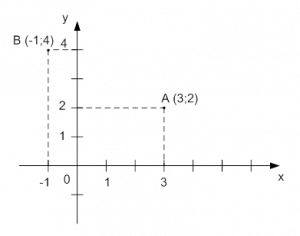
Рис. 2. Определение координат точек на координатной плоскости

Можно проделать это и наоборот, то есть нанести точку на плоскость зная её координаты.

Пример

1. Нанести точки по заданным координатам , А (2;5) В (3;-1)

Чтобы нанести точку , нужно отложить на оси число 2 и провести перпендикуляр к оси; на оси отложить число 5 и провести перпендикуляр. На пересечении этих перпендикуляров мы получаем точку с координатами .

Для точки необходимо отложить на оси 3 и провести перпендикулярную к оси прямую; на оси отложить число (–1) и провести перпендикулярную прямую. Пересечение перпендикуляров даст точку с координатами . (см. Рис. 3).

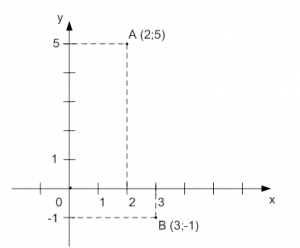
Рис. 3. Построение точек на координатной плоскости по заданным координатам

1. Нанести точки по заданным координатам , С (3;0) D (2;0)

Для построения точки отложите 3 на оси . Поскольку координата равна нулю, точка располагается на оси (см. Рис. 4).

Для построения точки отложите 2 на оси . Поскольку координата равна нулю, точка располагается на оси (см. Рис. 4).

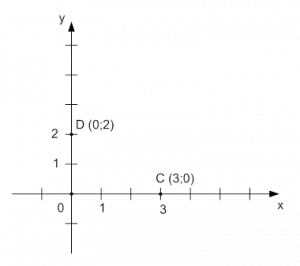
Рис. 4. Построение точек на координатной плоскости по заданным координатам

Следовательно, если координата равна нулю, то точка находится на оси Х, а если нулю равна координата Y , то точка располагается на оси .

Задача

1. Найти координаты точек A, B, C, D (см. Рис. 5).
2. Изобразить точки E ( -3; -2) F ( 5; 0) G (3; 4) H (0; -4) O (0; 0) .

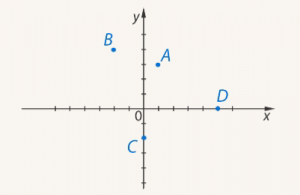
Рис. 5. Иллюстрация к задаче

Решение

1. Для определения координат точки необходимо провести через неё две прямые, параллельные координатным осям. Пересечение одной из линий с осью абсцисс даст координату , а пересечение другой линии с осью ординат будет означать координату . Следовательно, точка имеет координаты (см. Рис. 6).

Для определения координат точки той же схемой находят координаты, следовательно, точка имеет координаты .

Точка расположена на оси , и поэтому координата равна нулю, в то время как координата равна (–2). Следовательно, точка имеет координаты .

Точка расположена на оси , и координата равна нулю, а координата равна –5. Следовательно, точка имеет координаты .

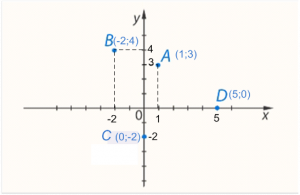
Рис. 6. Иллюстрация к задаче

1. Для построения точки откладываем на оси (–3) и проводим перпендикулярную прямую; на оси откладываем (–2) и проводим перпендикулярную направляющую. На пересечении перпендикуляров получим точку с координатами .

Координата точки равна нулю, и точка находится на оси . Отложите на оси число 5, результатом будет точка с координатами .

Для построения точки отложите 3 на оси и проведите перпендикулярную к оси линию; на оси отложите число 4 и проведите перпендикулярную линию. Пересечение перпендикуляров даст точку с координатами .

Координата точки равна нулю, поэтому точка расположена на оси . Отложите на оси число (–4), результатом будет точка с координатами .

Точка, для которой обе координаты равны нулю, располагается одновременно на оси и оси , то есть это точка пересечения осей (начало координат).

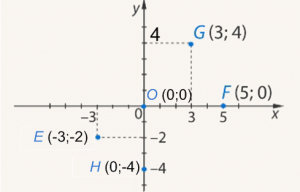
Рис. 7. Иллюстрация к задаче

Координатные четверти
Координатные оси разбивают плоскость на четыре сектора — четверти. Нумеруют четверти против часовой стрелки (см. Рис. 8).

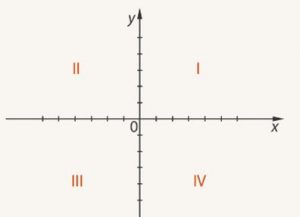
Рис. 8. Нумерация четвертей на координатной плоскости

Точка, имеющая положительную координату и положительную координату , располагается в первой четверти.

При отрицательной координате и положительной , точка располагается во второй четверти.

Точка с отрицательными и координатами расположена в третьей четверти.

При положительной координате и отрицательной , точка лежит в четвертой четверти.

Например, для точки с положительной координатой и отрицательной , она расположена в четвертой четверти.

Другие системы координат

Для того чтобы определить «адрес» точки посредством чисел, применяются и альтернативные системы координат.

Причины использования различных систем:

1. Размерность.

На уроке мы разбирали прямоугольную систему на плоскости с размерностью 2, где точка определена двумя координатами. Однако возможны иные размерности, например, размерность единица, где точка может двигаться только в одном измерении (вперед-назад или вверх-вниз). Пример — перемещение авто по ровной дороге или движение лифта. Для определения позиции потребуется всего одна координата. Этой координатой будет пройденное расстояние машиной (см. Рис. 9) или этаж лифта (см. Рис. 10).

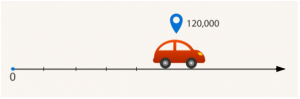
Рис. 9. В данном случае координата — это пройденное расстояние автомобилем

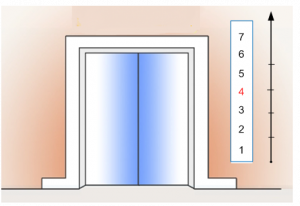
Рис. 10. В данном случае координата — это текущий этаж лифта

В математике такая система представлена числовой осью. Чтобы сделать прямую координатной осью, нужно отметить начало отсчета, масштаб и направление (см. Рис. 11). Одна координата позволяет однозначно определить положение точки.

Рис. 11. Координатная ось

Трехмерное пространство требует трех координат. Пример: в высотном здании с кинотеатром на каждом этаже место на билетах указано с помощью трех координат — этаж, ряд и номер кресла. Трехмерная система координат аналогична плоскости, с добавлением третьей оси (см. Рис. 12).

Рис. 12. Декартова система координат в пространстве

1. Альтернативный метод задания координат (полярная система на плоскости).

Используется ось , а для точки указывают расстояние до нее и угол с осью . Эти числа составляют координаты точки в этой системе (см. Рис. 13).

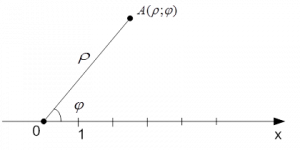
Рис. 13. Полярная система координат на плоскости

Существуют также сферическая и цилиндрическая системы для трехмерного пространства.

Таким образом, прямоугольная система часто применяется, но не единственна.

Список литературы

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. — М.: ЗШ МИФИ, 2011.
Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Учебное пособие для 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.