Делители и кратные
На сегодняшнем уроке мы изучим понятия множителей, делителей и кратных чисел. Научимся раскладывать числа на простые и составные множители, а также находить делители. В конце занятия решим несколько задач для закрепления материала.
Множитель и делитель
Одно и то же число можно представить по-разному. Например, числа 3 и 5, перемноженные, дают 15. Эти числа называются множителями числа 15. Однако их также можно использовать для деления, поэтому они являются делителями числа 15.
Таким образом, множитель и делитель — это два аспекта одного и того же. Чтобы число делилось на что-то, это что-то должно быть его множителем. Например, 15 делится на 5, потому что 5 — один из множителей 15.
Делители числа
Каждое число имеет как минимум два делителя: 1 и само себя. Например, число 1 делится только на 1, поэтому у него всего один делитель.
Простые и составные числа
Рассмотрим, как числа могут быть разложены на множители. Число 30 можно представить как произведение простых множителей: 2 × 3 × 5. Число 15 также можно разложить: 3 × 5. Простые числа — это те, которые нельзя разложить на множители, например, 2, 3 и 5. Составные числа — это те, которые можно разложить, например, 30 и 15.
Единица, хотя и может показаться простым числом, на самом деле не является ни простым, ни составным, так как у нее только один делитель — сама она.
Разложение на простые множители
Каждое число можно разложить на простые множители, и это разложение уникально, что называется основной теоремой арифметики. Например, для числа 30 разложение будет 2 × 3 × 5. Все эти простые множители также являются делителями числа.
Задание 1
Найдите все делители чисел: 70, 44 и 225.
70:
- Разложение: 2 × 5 × 7
- Делители: 1, 2, 5, 7, 10, 14, 35, 70
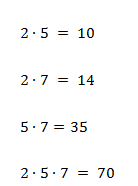
44:
- Разложение: 2 × 2 × 11
- Делители: 1, 2, 4, 11, 22, 44
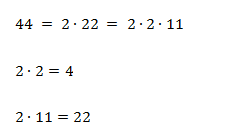
225:
- Разложение: 3 × 3 × 5 × 5
- Делители: 1, 3, 5, 9, 15, 25, 45, 75, 225
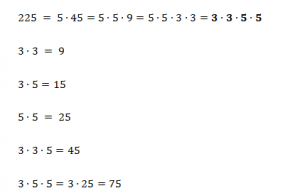
Задача 1
Чтобы проверить, является ли одно число делителем другого, можно просто выполнить деление. Например, проверим, является ли 12 делителем 2940.

Ответ: да, 12 является делителем 2940.
Кратное
Числа 3 и 5 — это множители числа 15, а 15 является кратным для 3 и 5. Если число делится на 3, то оно кратно 3. Например, 51 кратно 3, так как 51 делится на 3.
Задание 2
Рассмотрим число 14 586 237 и ответим на вопросы:
Какой наименьший делитель у этого числа?
- Ответ: 1 (делитель любого числа).
Какой наибольший делитель у этого числа?
- Ответ: само число 14 586 237.
Каково наименьшее кратное у этого числа?
- Ответ: само число 14 586 237.
Каково наибольшее кратное у этого числа?
- Ответ: кратных чисел бесконечно много, поэтому наибольшего не существует.
Задача 2
Решим задачу: на сколько равных команд можно разделить класс из 24 человек? Для этого найдем делители числа 24.
Разложим 24 на множители: 2 × 2 × 2 × 3. Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24.
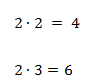
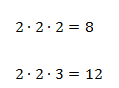
Ответ: 2, 3, 4, 6, 8, 12.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. «Математика 6». – М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. «Математика 6 класс. – Гимназия». – 2006.
- Депман И.Я., Виленкин Н.Я. «За страницами учебника математики». – М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. «Задания по курсу математика 5–6 класс». – М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. «Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ». – М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. «Математика: Учебник-собеседник для 5–6 классов средней школы». – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные ресурсы
- Интернет-портал «school-assistant.ru»
- Интернет-портал «matematika-na.ru»
Домашнее задание
- Папа и Денис измеряли расстояние от дома до речки. Какое расстояние от точки старта совпадет в первый раз, если шаг папы равен 90 см, а шаг Дениса – 70 см?
- На столе лежат пачки с 8 печеньями. Можно ли взять 8, 16, 24 или 18 печений, не раскрывая пачек?
Оцените урок:




