Вводная задача

Начнем с решения следующей задачи.

Задача № 1

У нас есть два экскурсионных автобуса. Первый автобус завершает экскурсию по городу за 2 часа, а второй — за 3 часа. Оба автобуса выехали из базы в 10 часов утра. В какое время они впервые встретятся на базе (см. рис. 1)?

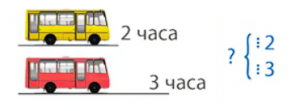
Решение

Первый автобус возвращается на базу каждые 2 часа, а второй — каждые 3 часа. Нам необходимо найти наименьшее число, которое делится на 2 и 3. Это число равно 6, так как меньшее число, удовлетворяющее этому условию, не существует.

Ответ: автобусы встретятся через 6 часов, то есть в 4 часа дня.

Определение наименьшего общего кратного

Наименьшее общее кратное (НОК) двух целых чисел $a$ и $b$ — это наименьшее натуральное число, которое делится на оба числа без остатка. В нашем случае НОК для 2 и 3 равен 6, что записывается как:

Также допустимо обозначение: $\text{НОК}(2;3)=6$.

Свойства НОК

1. НОК всегда больше или равен каждому из данных чисел.
2. Если одно число делится на другое, то НОК равен большему числу.
3. НОК можно выразить через НОД: НОК(a,b)=a⋅bНОД(a,b)НОК(a,b)=НОД(a,b)a⋅b​.

Пример №1: Нахождение НОК

Дано: числа 10 и 12.

Найти: $\text{НОК}(10,12)$.

Решение:

Разложим числа на простые множители:

• $10=2\cdot 5$
• 12=22⋅312=22⋅3

Теперь определим общие и уникальные множители:

• Общий множитель: $2$.
• Уникальные множители: $5$ и $3$.

Соберем все множители:

Ответ: $\text{НОК}(10,12)=60$.

Пример №2: Нахождение НОК

Дано: 36 и 48.

Найти: $\text{НОК}(36,48)$.

Решение:

Разложим на множители:

• 36=22⋅3236=22⋅32
• 48=24⋅3148=24⋅31

Общие и уникальные множители:

• Общие: 2222 и 3131.
• Уникальные: 2222 (из 48) и 3232 (из 36).

Соберем все:

Ответ: $\text{НОК}(36,48)=144$.

Пример №3: Нахождение НОК для трех чисел

Дано: 6, 12 и 15.

Найти: $\text{НОК}(6,12,15)$.

Решение:

Разложим на множители:

• $6=2\cdot 3$
• 12=22⋅312=22⋅3
• $15=3\cdot 5$

Общие и уникальные множители:

• Общий: $3$.
• Уникальные: 2222 (из 12) и $5$ (из 15).

Соберем:

Ответ: $\text{НОК}(6,12,15)=60$.

Пример №4: Нахождение НОК и НОД

Дано: 10 и 12.

Решение:

• НОК(10, 12) = 60 (как было показано ранее).
• НОД(10, 12) = 2 (общий делитель).

Связь НОК и НОД

Можно заметить, что в НОК не входит НОД чисел. Тогда выведем свойство: произведение любых двух натуральных чисел равно произведению их наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК)

Пример использования формулы:

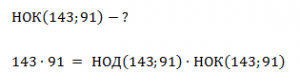
Используем алгоритм Евклида:

Пример использования формулы

Для чисел 10 и 12:

Повторение пройденного

Мы изучили определение НОК и научились находить его для двух и более чисел.

Список литературы

1. Виленкин Н.Я. «Математика. 6 класс. Учебник.» – 2014.
2. Никольский С.М., Потапов М.К. «Математика. 6 класс. Учебник.» – М.: 2012.
3. Никольский С.М. и др. «Алгебра. 6 класс. Учебник для общеобразовательных учреждений.» – М.: Просвещение, 2006.

Домашнее задание

1. Найдите НОК для следующих чисел: 8, 12, 14.
2. Найдите НОК(18; 24) и НОД(18; 24).
3. Найдите НОК для чисел 9, 15 и 21.

Дополнительные ресурсы

• Интернет-портал «math-prosto.ru»
• Интернет-портал «videouroki.net»