Применение распределительное свойство умножения
Распределительный закон
Выражение ![]() и выражение
и выражение ![]() являются эквивалентными, то есть:
являются эквивалентными, то есть:
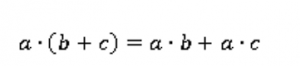
Это означает, что можно умножать всю сумму на число, а можно – каждое слагаемое отдельно. Результат будет одинаков.
Это верно и для большего числа слагаемых:
![]()
Также возможен переход от второго выражения к первому:
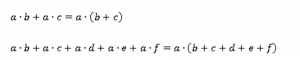
Переход от первого выражения ко второму называется раскрытием скобки, а переход от второго к первому – вынесением общего множителя за скобки.
Само равенство этих выражений называют распределительным законом.

Задача 1
Выполните умножение:
1. 12 * 11
Для того чтобы было проще вычислить произведение данных чисел, представим 12 как сумму чисел 10 и 2:
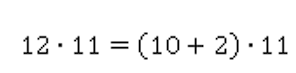
Применим распределительный закон, и вычисления станут проще:
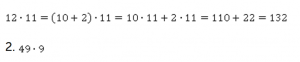
Число 49 можно представить как разность чисел 50 и 1:
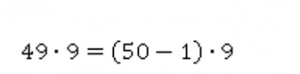
Далее воспользуемся распределительным законом:
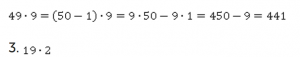
Представим число 19 как разность чисел 20 и 1, далее применяем распределительный закон:
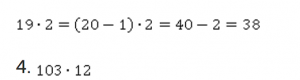
Представим число 103 как сумму чисел 100 и 3, далее применяем распределительный закон:
![]()
Таким образом, перемножение двух больших чисел можно производить в уме, используя при этом распределительный закон.
Умножение смешанной дроби на число с помощью распределительного закона
Представим, что нам необходимо умножить смешанную дробь на число, например:
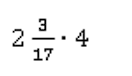
1 способ:
Можно смешанную дробь записать в виде обыкновенной правильной дроби:
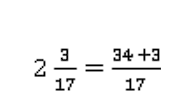
Тогда:
![]()
2 способ:
Смешанная дробь – это запись суммы целого и дробного числа, поэтому можно поставить знак плюс между целой и дробной частью:
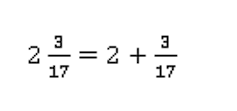
Тогда:
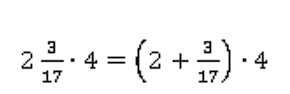
Воспользуемся распределительным законом:
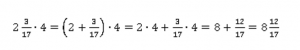
Задача 2
Выполните умножение:
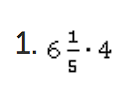
Между целой и дробной частью смешанной дроби поставим знак плюс, а далее применим распределительный закон:
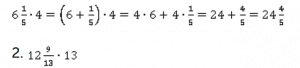
Между целой и дробной частью смешанной дроби поставим знак плюс, а далее применим распределительный закон:
Задача 3
Вычислите:
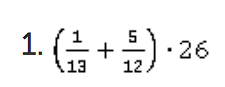
Для вычисления данного выражения воспользуемся распределительным законом:
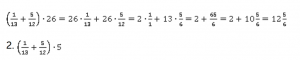
Для решения данного выражения нет смысла раскрывать скобки, так как при этом ничего не сократится, а вид дробей станет сложнее. Поэтому в данном случае не целесообразно применять распределительный закон.
Сначала произведем сложение двух дробей в скобках, а далее полученную сумму умножим на 5.
![]()
Следовательно, применять распределительный закон уместно в том случае, если он упростит вычисления.
Список литературы
- Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А. Г., Полонский В. В., Якир М. С. Математика для 6 класса. – Гимназия, 2006.
- Депман И. Я., Виленкин Н. Я. За страницами учебника математики. – М.: Просвещение, 1989.
- Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика: Учебник-собеседник для 5–6 классов. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные онлайн-ресурсы
- Интернет-ресурс «school-assistant.ru» (Источник)
- Интернет-ресурс «for6cl.uznateshe.ru» (Источник)
- Видеохостинг «youtube.com» (Источник)
Домашнее задание
Выполните задания 537, 538, 540 (стр. 88–89) из книги Виленкина Н. Я., Жохова В. И., Чеснокова А. С., Шварцбурда С. И. Математика 6. Ссылка на задания.
Продолжительность жизни березы составляет 150 лет. Сосна живет в 1,5 раза дольше березы, а мамонтово дерево существует в 5 раз дольше сосны. Какова продолжительность жизни мамонтова дерева?
Найдите значение выражения: [укажите выражение].
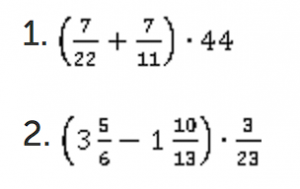
Оцените урок:





