Введение

Мы часто находим часть от числа или наоборот, вычисляем число по его части:

Например:

Сколько будет 1/2 от 5 км? Понятно, что полпути – это 2,5 км (см. Рис. 1).

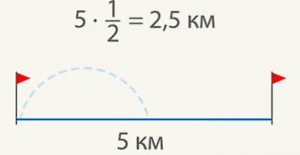
Рис. 1. Иллюстрация к примеру

Или наоборот:

Треть арбуза весит 4 кг, сколько весит весь арбуз? Чтобы 1/3 была 4 кг, весь арбуз должен весить 12 кг (см. Рис. 2).

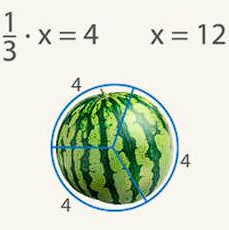
Рис. 2. Иллюстрация к примеру

Все вычисления нам тоже уже знакомы в таких задачах – это умножение и деление целых чисел и дробей.

Сейчас мы разберем, какие задачи на эту тему бывают и каков их общий метод решения, алгоритм.

Когда мы рассматриваем дробь (часть) от какого-то количества, то мы видим три величины:

• Исходное количество. Обозначим его A
• Дробь, часть, проценты. Обозначим эту дробь q.
• Дробная часть исходного количества. Обозначим это количество B.

Например:

• A = 60 – количество минут в одном часе.
• Дробь – q = 1/3.
• B = 20 – количество минут в одной трети часа.

Все эти три величины связаны одним равенством:

60 * 1/3 = 20

Или в общем виде:

A * q = B

Эта строчка A * q = B описывает очень простой факт: Если некое количество умножить на дробь, то получим дробь от этого количества.

Этой записи достаточно, чтобы решить любую задачу по теме «дробь от числа», любую задачу на проценты.

То есть, у нас появляется алгоритм. Причем, очень простой алгоритм для решения задач на дроби от числа, на проценты.

Итак, у нас три величины, связанные равенством. Если известны две, то всегда можно найти третью. В зависимости от того, какая величина неизвестна, получаем три типа задач. На самом деле, различия очень невелики, алгоритм решения один и тот же.

Первый тип: неизвестно B

То есть мы знаем исходное количество и дробь. Нужно найти эту дробь от исходного числа.

Пример 1

Сколько будет 1/5 часа?

A = 60

q = 1/5

B = ?

A * q = B

60 * 1/5 = B

60 * 1/5 = 12

Ответ: 12 минут.

Пример 2

Полуторалитровая бутылка наполнена на 3/4. Сколько там воды?

A = 1/5

q = 3/4

B = ?

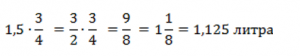
Ответ: 1,125 литра.

Пример 3

Если положить 20 000 рублей в банк под 13 % годовых, сколько денег будет на счету через год?

Банк за год добавит к исходной сумме 13 % от нее. Найдем эту добавку. Исходная сумма – 20 000. 1 % – это 0,01. 13 % – это 0,13.

То есть добавка – это 0,13 от 20 000. Найдем ее.

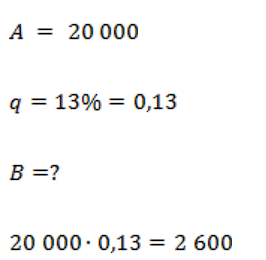
Мы нашли добавку. В задаче спрашивалось, сколько всего будет на счету.

Сложим исходную сумму и добавку

На самом деле, такую задачу решают не в два действия, а в одно.

Банк добавит 13 %. Значит, сколько процентов от исходной суммы будет через год? Исходная сумма – 100 % и еще 13 %. Итого 113 %. То есть нам нужно найти 113 % от исходной суммы.

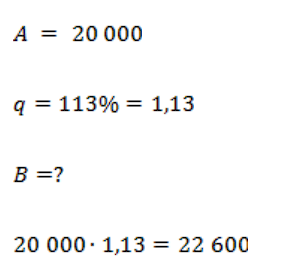
Ответ: 22 600 рублей.

У кого вызвала затруднение работа с процентами, посмотрите урок на эту тему, перейдя по ссылке.

Второй тип: неизвестно A

Мы не знаем, какое было число изначально, но знаем, сколько получилось, когда от него взяли некую дробь. Нужно найти исходное.

То есть мы не знаем A, но знаем q и B.

Тогда A = B/q

Пример 4

Дедушка 3/4 своей жизни провел в деревне, что составило 63 года. Сколько лет дедушке?

Нам неизвестно исходное число – возраст. Но мы знаем долю 3/4  и сколько лет эта доля составляет от возраста. Составляем равенство. Оно имеет вид уравнения с неизвестной A. Выражаем A и находим его.

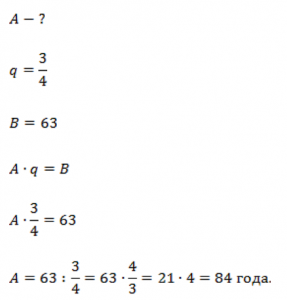
Ответ: 84 года.

Не очень реалистичная задача. Вряд ли дедушка будет выдавать такую информацию о своих годах жизни.

А вот следующая ситуация очень распространена.

Пример 5

Скидка в магазине по карте 5 %. Покупатель получил скидку 30 рублей. Какова была стоимость покупки до скидки?

Мы не знаем изначального числа – стоимости покупки. Но знаем дробь (проценты, которые написаны на карте) и сколько составила скидка.

Составляем нашу стандартную строчку. Выражаем неизвестную величину A и находим ее.

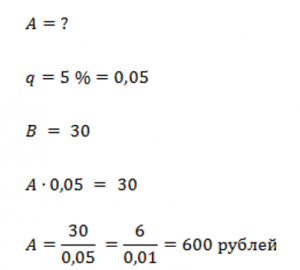
Ответ: 600 рублей.

Пример 6

Часто мы сталкиваемся с ситуацией, когда известна не сумма скидки, а цена, которую мы заплатили после применения этой скидки. В этом случае вопрос остается прежним: сколько бы мы заплатили без скидки?

Предположим, у нас есть 5%-я дисконтная карта. Мы показали ее на кассе и заплатили 1140 рублей. Какова была полная стоимость без скидки?

Чтобы решить эту задачу одним шагом, немного изменим формулировку. Поскольку у нас 5%-я скидка, то мы платим 95% от полной цены.

Таким образом, нам неизвестна исходная стоимость, но мы знаем, что 95% от нее составляет 1140 рублей.

Теперь применим алгоритм, чтобы вычислить начальную стоимость.

Ответ: 1200 рублей.

Третий тип: неизвестно q

В этом случае мы знаем исходное число и конечное значение, но не знаем, какую долю от исходного числа мы взяли. Именно эту долю необходимо определить.

Пример 7

Какую долю составляет 18 от 75? И сколько это в процентах?

Алгоритм остается прежним – мы записываем наше уравнение. Важно не перепутать, какое число является исходным, а какое – результатом взятия доли.

Исходное число – 75, а неизвестная нам часть – это 18.

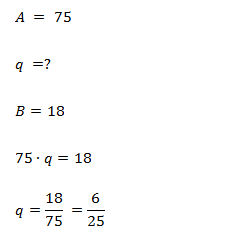
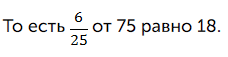
Если ответ нужно дать в процентах, то 6/25 нужно перевести в десятичную дробь.

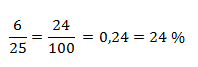
То есть 18 – это 24 % от 75.

Ответ: 24 %.

Такие задачи часто могут встречаться в реальной жизни.

Пример 8

Например, как измерить соленость морской воды?

Очень просто. Возьмем килограмм морской воды. И выпарим ее всю. Останется сухая соль. Взвесим ее. Получилось, например, 52 г.

Что мы знаем?

Что изначальное количество 1 кг = 1000 г. Какую-то неизвестную нам долю q составляет соль. Эта доля составляет 52 г. Найдем, какую долю в общей массе составляет соль.

Применяем наш алгоритм и находим q.

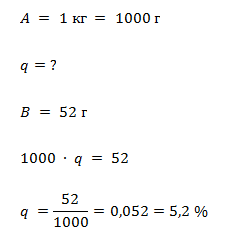
Если бы мы взяли 2 кг воды и всю ее выпарили, то получили бы и соли в два раза больше. Доля q не изменилась (увеличили числитель и знаменатель в два раза). То есть доля q не зависит от количества воды, которое мы берем для исследования. Эта доля и называется соленостью воды.

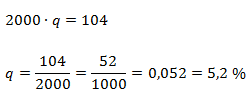
Ответ: 5,2 %.

Заключение

Для решения задач, связанных с долями и процентами, существует единый и простой алгоритм.

1. Определите, что является исходным количеством, какую долю вы берете и каков размер этой доли.
2. Запишите основное уравнение, связывающее три величины.
3. Найдите неизвестную величину, решив уравнение.

Список литературы

1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А. Г., Полонский В. В., Якир М. С. Математика 6 класс. – Гимназия, 2006.
3. Депман И. Я., Виленкин Н. Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А. Н., Чайковский И. В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А. Н., Сочилов С. В., Чайковский К. Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные ресурсы

• Интернет-портал «school-assistant.ru»
• Интернет-портал «math-prosto.ru»
• Интернет-портал «matematika-na.ru»

Домашнее задание

1. Математика. 6 класс / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – М.: Мнемозина, 2011. Стр. 104–105. п.18. № 680; № 683; № 783 (а, б).
2. Математика. 6 класс / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – М.: Мнемозина, 2011. № 656.
3. В программе спортивных школьных соревнований были прыжки в длину, прыжки в высоту и бег. В соревнованиях по бегу приняли участие 5/12 всех участников соревнований, в прыжках в длину – 30 % всех участников, и в соревнованиях по прыжкам в высоту – оставшиеся 34 ученика. Найдите число участников соревнований.