На этом уроке учащиеся узнают, как найти отношение между двумя или более числами и сравнить объекты на основе этого отношения.

Вы будете практиковаться в решении всех форм задач на отношения, включая задачи на проценты и задачи на отношения без конкретных значений. Если вам трудно понять эту тему, вы можете посмотреть уроки: измерение и связь между числом и геометрией. Часть 1: Измерения в геометрии. Свойства фигур» „Тригонометрия“

Введение

Натуральные числа имеют множество применений. 5 яблок. 3 машины. 2. Представляют собой порядок. Пятый дом находится после третьего дома и перед девятым домом; 3. Имена. Номера футболок и телефонов спортсменов являются аналогами имен. Аналогично, дроби имеют различные назначения: 1. для обозначения количества. Пол-литра молока, четверть часа, две трети; 2. для сравнения двух чисел. Брату 5 лет, сестре 3 года. Старший брат в один раз больше младшей сестры. Эта дробь не представляет собой количество. Сравнение одного числа с другим. Такое сравнение называется отношением. Оно показывает, во сколько раз одно число больше (или меньше) другого. Рассмотрим такую ситуацию. Художник видит дом и рисует его на бумаге. Мы понимаем, что это один и тот же дом. Но на бумаге он во много раз меньше. Что же остается неизменным? Соотношение высоты и ширины дома остается неизменным. Другими словами, если реальная высота дома в три раза больше ширины, то и на рисунке она будет такой же. Если высота дома составляет 15 метров, а ширина — 5 метров, то высота и ширина на рисунке могут быть 15 см и 5 см, или 30 см и 10 см, но не 10 см и 5 см.

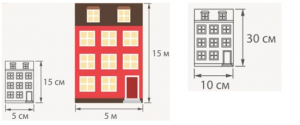
Если разделить высоту на ширину дома, то мы получим их отношение.

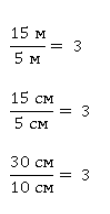
Отношение везде было одинаковым.

Отношение может рассматриваться не только для двух, но и для любого количества величин.

Пример 1

Лотерейный билет стоил 100 рублей. Маша внесла 10 рублей, Петя – 20 рублей, Вася – 30 рублей и Вика – 40 рублей. Всего 100 рублей. Билет выиграл. Выигрыш 1000 рублей. Как справедливо разделить выигрыш?

Справедливо будет разделить в таком же отношении. Запишем отношения взносов.

10:20:30:40

В таком отношении у нас разделено 100 рублей.

Понятно, что, чтобы в таком же отношении разделить 1000 рублей, нужно все увеличить в 10 раз.

100:200:300:400

Это и будет справедливым.

В случае отношения двух чисел можно использовать и двоеточие, и дробную черту:

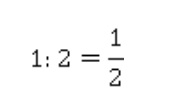
В случае трех и более чисел используем только двоеточие:

1:2:3

Отношение двух чисел

Обычно отношение двух чисел используют в двух случаях:

1. Отношение двух различных величин

Отношение высоты дома к его ширине.

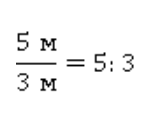
Отношение роста или возраста двух человек.

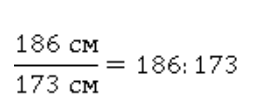
2. Отношение частей или части и целого

Высота основной части дома 5 метров, крыши – 3 метра (см. Рис. 2).

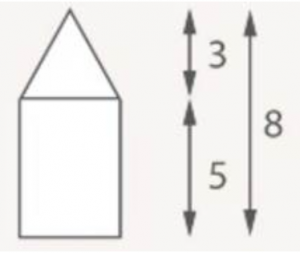
Рис. 2. Отношение частей или части целого на примере дома

Можем записать различные отношения частей или частей и целого.

Крыша к основной части: 3:5

Крыша ко всему дому: 3:8

Основная часть ко всему дому: 5:8

Задача 1

Масса слона – 5 т, масса кита – 80 т. Найти отношение их масс.

Чтобы найти отношение, нужно одну величину разделить на другую. Отношение массы слона к массе кита составляет 5:80. В принципе, задача уже решена. Но это отношение можно упростить. Разделим обе части на 5. Получим отношение 1:16.

То же самое можно записать в виде дроби.

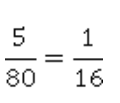
Можно было поступить наоборот: разделить массу кита на массу слона.

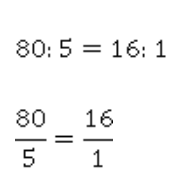
1:16 – отношение массы слона к массе кита

16:1 – отношение массы кита к массе слона

Такие отношения называют взаимно-обратными.

Оба отношения показывают нам одно и то же. Кит в 16 раз тяжелее слона.

Ответ:1:16, 16:1.

Задача 2

Весь путь составляет 30 км. Пройдено 6 км.

Каково отношение пройденного пути ко всему пути; к оставшемуся? (См. Рис. 3.)

Рис. 3. Иллюстрация к задаче 2

Разделим пройденный путь на весь путь.

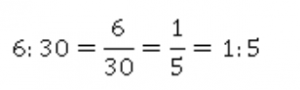
Отношение 1:5. Это означает, что пройденный путь в 5 раз меньше всего пути. Чаще мы в такой ситуации говорим, что пройденный путь составляет 1/5 от всего пути, и используем дробь.

Отношение пройденного пути к оставшемуся говорит нам, что осталось в 4 раза больше, чем пройдено.

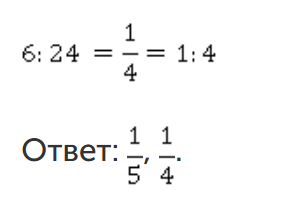
Задача 3

Сколько процентов составляет 3 минуты от 1 часа?

Задачи на проценты тоже являются задачами на отношение двух величин.

Найдем отношение 3 минут к часу.

Переведем часы в минуты, чтобы у нас были одинаковые единицы измерения (см. Рис. 4).

Рис. 4. Иллюстрация к задаче 3

3 мин : 60 мин

Так как единицы измерения одинаковые, то различие только в количестве, значит, можно рассмотреть только отношение чисел.

3 : 60

Сократим на 3. Получаем:

1 : 20 или 1/20

Мы можем сказать, что 3 мин относятся к 1 ч, как 1 : 20.

Или: 1 час в 20 раз больше, чем 3 мин.

Или: 3 минуты составляет 1/20 от часа.

Так как в условии просили дать ответ в процентах, то надо дробь 1/20  перевести в проценты. Проценты – это сотые. Переведем нашу дробь в сотые. Домножим числитель и знаменатель на 5. Получим .

Три минуты – это 5 % часа

Ответ: 5 %.

Нахождение отношения без точного значения величин

Не обязательно знать, чему равны две величины, чтобы найти их отношение.

В самом деле, если пройдена 1/3 пути, то каково отношение пройденного пути к оставшемуся?

Пройдена 1/3, осталась 2/3. Оставшийся путь в два раза больше.

То есть отношение пройденного к оставшемуся равно 1:2.

Технически это получить не сложно.

Разделим 1/3 на 2/3.

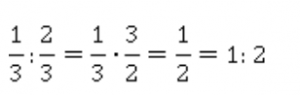
Деление на дробь равносильно умножению на обратную (перевернутую) дробь.

После сокращения получаем 1/2 или отношение 1:2.

Заключение

Итак, подведем итог.

• Чтобы найти отношение двух величин, нужно одну разделить на другую. Это можно записать с помощью знака деления или дробной черты.

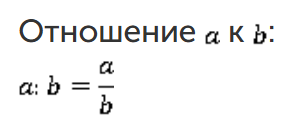
• Величины должны быть выражены в одних единицах

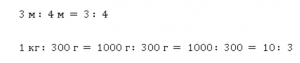
• Величины сами могут быть дробями или процентами

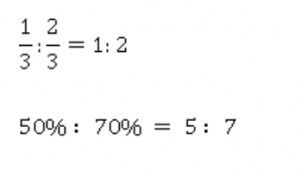
Отношения трех и более чисел

Задача 1

Треугольник, у которого стороны относятся как 3:4:5, обязательно имеет прямой угол. Его использовали древние египтяне, чтобы начертить на земле прямой угол. Треугольник так и называется – египетский.

Размеры могут быть разные, но отношение одно и то же (см. Рис. 5).

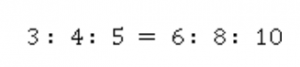
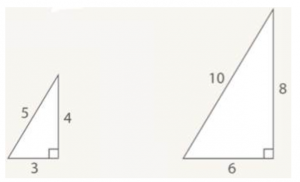
Рис. 5. Египетский треугольник

Задача 2

Коробка имеет размеры: 1,2 м, 60 см, 90 см.

Дом имеет размеры: 8 м, 4 м, 6 м.

Можно ли сказать, что у коробки и дома одинаковая форма (или, еще говорят, одинаковые пропорции)?

Запишем отношения размеров:

Кажется, что они разные.

Но для отношений выполняется такое же свойство, как и для дробей: все числа можно умножить или разделить на одно и то же число.

Разделим в первом отношении все на 10:

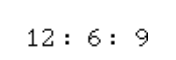
И еще на три:

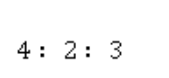
Дальше не упрощается.

Теперь второе соотношение:

Разделим все на два.

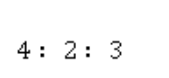
Соотношения оказались одинаковыми.

Ответ: коробка и дом имеют одинаковую форму, одинаковые пропорции.

Задача 3

Отношения возрастов сестры, брата, мамы и папы составляет: 2:5:18:19.

Сестре 4 года. Сколько лет всем остальным?

Все члены отношения можно умножить или разделить на любое число. Чтобы первый член отношения стал 4, умножим все члены отношения на 2.

4:10:36:38

Все, мы решили задачу.

Сестре – 4 года, брату – 10 лет, маме – 36 лет, папе – 38 лет.

Ответ: 10, 36, 38.

Задача 4

В бригаде первый рабочий работал 3 дня, второй – 5 дней, третий – 6. Бригада получила оплату 35 000 рублей. Необходимо разделить деньги между рабочими в отношении потраченного времени.

Отношение потраченных дней равно 3:5:6. Значит, и гонорар нужно разделить в таком же отношении. Справедливо, если каждый работник получает одинаковую плату за один день работы.

Обозначим ее x. Тогда первый получит 3x, второй 5x, а третий 6x. В сумме это должно быть 35 000.

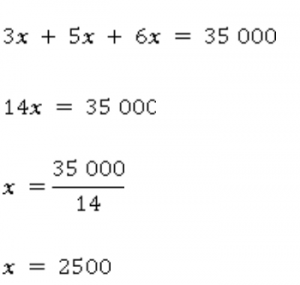
Тогда дневная оплата одному рабочему составляет 2500 рублей.

Осталось посчитать для каждого:

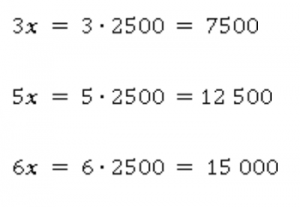
Ответ: 7500 рублей, 125 00 рублей, 15 000 рублей.

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – Москва: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика для 6 класса. – Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – Москва: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по математике для 5-6 классов. – ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика для 5-6 классов: пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: учебник-собеседник для 5-6 классов средней школы. – Москва: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные интернет-ресурсы

• Интернет-портал «math-prosto.ru» (Источник)
• Интернет-портал «school-assistant.ru» (Источник)
• Интернет-портал «matematika-na.ru» (Источник)

Домашнее задание

1. Определите отношение: 

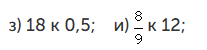
2. Труба была разделена на два отрезка. Длина первого отрезка составляет 0,8 метра, а длина второго — 2,4 метра. Определите, какую долю от общей длины трубы занимает первый отрезок и какую долю занимает второй отрезок. Также выясните, какую долю длины второго отрезка составляет длина первого отрезка.

3. В 3-литровую банку было налито 2 литра воды, в которую добавили 40 граммов соли. Определите процентное содержание соли в воде. Как изменится это значение, если через два дня из банки испарится 300 граммов воды? (Учтите, что 1 литр воды весит 1 килограмм.)