На этом уроке мы обсудим шар — простейшую геометрическую фигуру, форму которой имеют многие предметы, знакомые нам с детства. Шар считается идеальным телом. Но почему? В ходе занятия мы ответим на этот вопрос с математической точки зрения. Вы познакомитесь с определением шара, узнаете о таких понятиях, как радиус и диаметр, а также о том, как эти величины связаны между собой.

Введение

Точки, отрезки и прямые — это идеализированные модели, которые не встречаются в реальной жизни, но они очень полезны для изучения объектов, напоминающих их.

Это не удивительно: например, мы говорим «стол». Столов существует множество, и непонятно, о каком именно идет речь. Тем не менее, фраза «сижу за столом» понятна всем, потому что у каждого из нас есть представление о столе.

Аналогично можно говорить и о шаре. В природе и технике много объектов, которые имеют форму шара: воздушные шары, капли, планеты, футбольные мячи…

Все эти предметы различаются, их формы немного отличаются, но у них есть общее — они все похожи. Поэтому мы сосредоточимся на изучении математической модели этих объектов — шара.

Сфера и шар

Когда мы говорили о круге, мы упоминали два объекта: сам круг и его границу — окружность. Хотя в повседневной речи люди часто путают круг и окружность, они представляют собой разные понятия, для которых и существуют различные названия. Круг — это плоская фигура с площадью, тогда как окружность — это линия, ограничивающая круг. У окружности нет площади, но есть длина. (См. Рис. 1.)

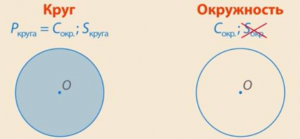
Так и мы, когда начинаем говорить про шар, то у нас тоже возникают два объекта. И им тоже дали отдельные названия. Это сам шар и его поверхность. Ее иногда так и  называют «поверхность шара», но у нее есть отдельное название – «сфера».

Почему сфера (поверхность шара) важна? Рассмотрим это вот на таком примере.

Люди живут на Земле. Они живут на поверхности огромной шарообразной планеты, то есть на сфере. (См. Рис. 2.)

Рис. 2. Поверхность Земли

Когда мы задаем вопрос: «Каково расстояние от Москвы до Нью-Йорка?», мы имеем в виду, каково это расстояние для транспорта, то есть расстояние, измеренное на сфере. На само же деле две эти точки ближе, если измерять по прямой. (См. Рис. 3.)

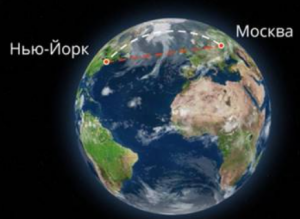
Рис. 3. Расстояние на сфере и по прямой

Итак, давайте теперь точнее опишем, что же мы называем шаром и сферой.

Отметим точку, это будет центр. Возьмем произвольный отрезок с одним концом в выбранном центре. Его длину обозначим . Все точки пространства, куда дотянется второй конец отрезка, образуют сферу. (См. Рис. 4.)

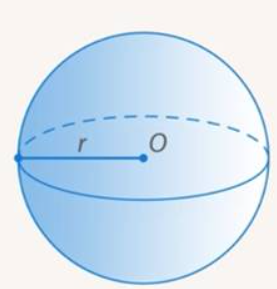
Рис. 4. Сфера

Если взять не только точки сферы, но и все точки внутри нее, то получится шар. (См. Рис. 5.)

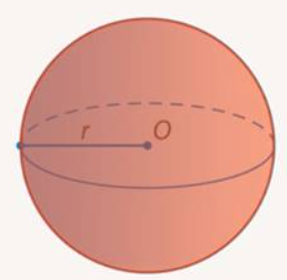
Рис. 5. Шар

Отрезок, который мы использовали для определения шара, называют радиусом. (Рис. 6.) Длину этого отрезка тоже называют радиусом. То есть под радиусом понимают две вещи: и отрезок, и число (длину отрезка).

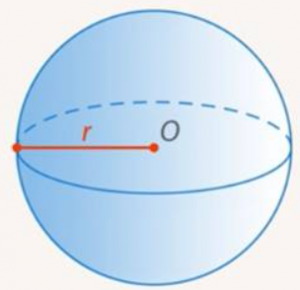
Рис. 6. Радиус шара

Отрезок, проходящий через центр, соединяющий две точки на сфере, называют диаметром шара. Диаметр шара равен двум радиусам. Обозначают диаметр буквой , маленькой или большой. (См. Рис. 7.)

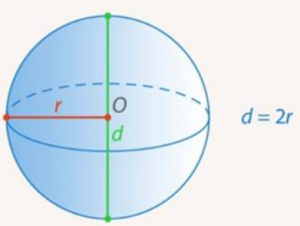
Если изложить это кратко, то получим следующие определения:

Сфера — это совокупность точек, находящихся на заданном расстоянии от определенной точки, которая называется центром. Это расстояние называется радиусом сферы.

Шар — это набор точек, находящихся на расстоянии не больше заданного от определенной точки, также называемой центром. Это расстояние называется радиусом шара.

Центр и радиус для шара и его ограничивающей сферы совпадают.

Шар и круг

Шар имеет много общего с плоской фигурой — круг, так же как куб напоминает квадрат.

 1. У круга, как и у шара, есть центр и радиус. Окружность выполняет для круга ту же роль, что и сфера для шара — она является его границей. (См. Рис. 8.)

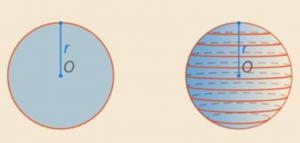
Рис. 8. Иллюстрация к пункту 1

2. Определения круга и шара очень похожи, в обоих случаях это множество точек, удаленных не далее чем на радиус от центра. Разница только в том, что круг находится на плоскости, а шар – в трехмерном пространстве. (См. Рис. 9.)

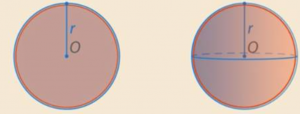
Рис. 9. Иллюстрация к пункту 2

3. Если круг начать вращать, используя диаметр как ось вращения, то получится шар. (См. Рис. 10). А если окружность – то сфера. (См. Рис. 11.)

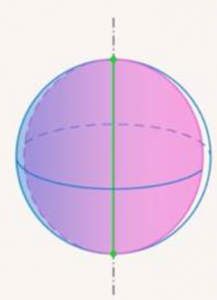
Рис. 10. Круг образует шар

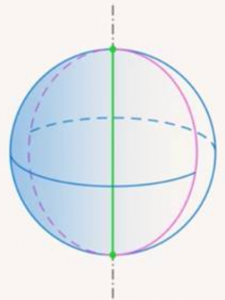
Рис. 11. Окружность образует сферу

4. Если шар пересечь плоскостью, то получится круг. (См. Рис. 12.1)

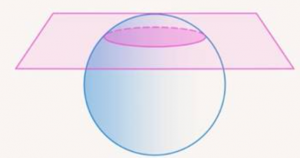
Рис. 12.1. Иллюстрация к пункту 4

В зависимости от того, как проходит плоскость, круги будут получаться разных размеров.

Если плоскость проходит через центр шара, то полученный в сечении круг называют большим кругом. (См. Рис. 12.2)

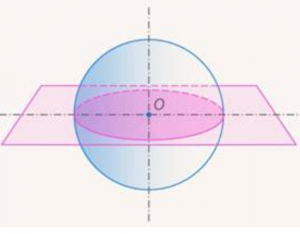
Рис. 12.2. Большой круг

Географические координаты

Сечения плоскостями земного шара используются для задания системы координат на нем.

Вот Земля. Сверху Северный полюс, снизу Южный. (См. Рис. 13.)

Чтобы обозначать или передавать местоположение на Земле, необходимо установить систему координат. Мы решили сделать это следующим образом.

Если представить Землю, пересеченную вертикальными плоскостями, проходящими через оба полюса, то мы получим большие круги, а на поверхности — окружности. Эти окружности, или их половины от полюса до полюса, называются меридианами. По меридианам определяется одна из координат — долгота. Для этого необходимо выбрать один меридиан в качестве начальной точки отсчета, а остальным присвоить числовые значения, исходя из этого нулевого меридиана. В настоящее время общепринято считать нулевым меридианом тот, который проходит через обсерваторию в Гринвиче, районе Лондона. Его называют Гринвичским меридианом. (См. Рис. 14.)

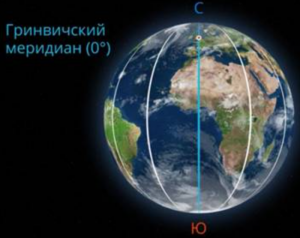
Рис. 14. Меридианы

Вторая часть окружности нулевого меридиана считается равной . Для перпендикулярного большого круга восточный меридиан считается , западный . (См. Рис. 15.)

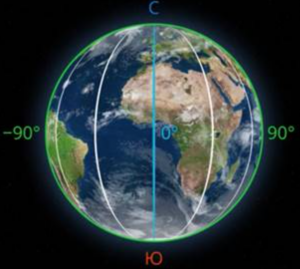
Рис. 15. Восточный и западный меридианы

Теперь, если Землю пересекать параллельными горизонтальными плоскостями, мы будем получать окружности разного размера на поверхности. Их назвали параллелями. В отличие от меридианов среди параллелей только одна является окружностью большого круга. Ее называют экватор. И она принята за ноль для другой координаты – широты. (См. Рис. 16.)

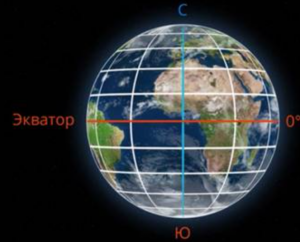
Рис. 16. Параллели

Вверх, на север, принято считать положительное направление. Самая большая координата получается на Северном полюсе: . На юг – отрицательные координаты: до , которая соответствует Южному полюсу. (Рис. 17.)

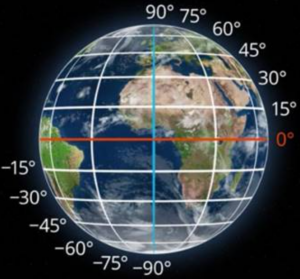
Рис. 17. Координаты параллелей

Теперь каждая точка на земной сфере получает две числовые координаты, зная которые, можно абсолютно точно указать место, о котором идет речь. Обычно используют термины: северная широта – для обозначения положительного направления широт, южная широта – для обозначения отрицательного направления широт; восточная долгота – для обозначения положительного направления долгот, западная долгота – для обозначения отрицательного направления долгот. (См. Рис. 18.)

Рис. 18. Термины

Так, например, географические координаты центра Москвы:  северной широты,  восточной долготы. (См. Рис. 19.)

Рис. 19. Координаты Москвы

Дети капитана Гранта искали своего отца по записке в бутылке, где были указаны его географические координаты. Неприятность была в том, что одна координата, а именно долгота, оказалась размыта водой. Осталась только одна координата –  параллель южной широты. (См. Рис. 20.)

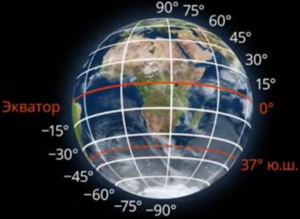
Рис. 20. 37 параллель южной широты

Им пришлось проплыть и пройти пешком вдоль этой параллели огромное расстояние, прежде чем они нашли отца. Ну а если бы обе координаты сохранились, то и приключенческой книги не получилось.

Изображение шара

Потренируемся изображать шар. Сначала построим окружность. Центр окружности будет являться и центром шара. (См. Рис. 21.)

Рис. 21. Построили окружность

Чтобы показать объем, что это именно шар, чертят хотя бы один большой круг, чаще горизонтальный. (См. Рис. 22.) Теперь уже понятно, что изображен шар.

Рис. 22. Шар

Можно добавить еще один большой круг, вертикальный. (См. Рис. 23.)

Рис. 23. Дополнительный большой круг