Сравнение чисел
На этом уроке мы научимся сравнивать положительные и отрицательные числа, а также изучим несколько правил для их сравнения. Кроме того, мы рассмотрим, как отрицательные числа применяются в математике и в реальной жизни. Мы введем новое понятие «модуль» и научимся использовать его для сравнения отрицательных чисел, а также решим несколько задач на эту тему.
Введение
Положительные числа используются для обозначения различных количеств – как целых, так и дробных. Например, три яблока или полтора литра молока.
Отрицательных количеств в действительности не существует. Отрицательные числа служат инструментом для упрощения расчетов. Например, такие случаи:
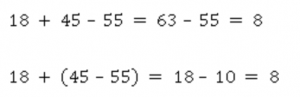
Ключ имеет одну функцию – открывать или закрывать замок. Если нет замка, то ключ практически бесполезен, ему трудно найти применение.
Так и отрицательные числа – без самого «замка», без различных математических расчетов они используются не очень много.
Сравнение чисел
Как мы понимали, что одно положительное число больше другого?
Из 8 яблок можно взять 5 яблок. 5 – это часть восьми. Поэтому мы с вами и знаем, что 5 меньше 8.
Но про числа -8 и -5 нельзя сказать, что одно – часть другого. Отрицательного количества не существует.
Но что же такое тогда отрицательное число?
Отрицательное число – это и число, и знак вычитания.
Что значит к 10 добавить -8?
Это значит вычесть 8.
А добавить -5 – означает вычесть 5.
Мы к одному и тому же числу 10 добавили два разных отрицательных. Во втором случае результат был больше. Естественно считать, что второе отрицательное число было больше.
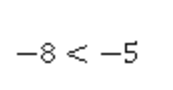
То есть чем большее число мы вычитаем, тем меньше будет результат. Это очевидно, но если это записать на языке отрицательных чисел, то мы и получим правила их сравнения.
Правила сравнения чисел
Сформулируем теперь правила, как сравнивать отрицательные числа друг с другом или с положительными.
1. Все отрицательные числа меньше всех положительных. Между ними находится ноль. То есть ноль меньше любого положительного числа, но больше любого отрицательного.
Почему это так?
Если мы к числу прибавляем положительное число, то число увеличится; если ноль, то не изменится; если вычтем положительное, то число уменьшится. Но добавление отрицательного числа и означает вычитание.
2. Чем больше положительное число, тем меньше противоположное ему отрицательное число.
Например, ![]()
Это и понятно, ведь если отнять 20, то результат будет меньше, чем если отнять 10.
Если у числа не обращать внимания на знак, то получающееся число мы называем модулем.
У числа -23 и у 23 одинаковые модули, 23.
Тогда про отрицательные числа можно сказать и так.
Из двух отрицательных чисел меньше то, у которого больше модуль.
Порядок чисел
Вернемся к такой функции чисел, как порядок.
Когда мы едем по дороге, то через равные промежутки нам встречаются километровые столбы с обозначением пройденного расстояния. В математике мы сделали аналог такой дороги – числовой луч. Числа на луче соответствуют точкам, и наоборот.
«Одно число больше другого» теперь означает, что «одна точка правее другой». Чем правее точка, тем больше соответствующее ей число, мы это число называем координатой (см. рис. 1).
![]()
Рис. 1. Числовой луч
Теперь, когда у нас есть отрицательные числа, мы можем расширить нашу модель. Вместо луча мы уже берем целую прямую и влево от нуля откладываем отрицательные числа.
Правило «чем правее точка, тем больше число» сохраняется и для левой части прямой.
Точка с координатой -5 правее точки с координатой -8. Это эквивалентно тому, что -8 < -5.
Шкала уличного термометра – пример, как такую числовую прямую можно применить в жизни (см. рис. 2).
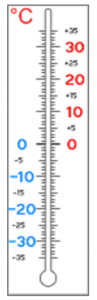
Рис. 2. Термометр
Пример
Потренируемся сравнивать числа.
1. 25 641 и -25 642
Тут все просто: отрицательное число всегда меньше положительного.
![]()
2. -25 641 и -25 642
Оба числа отрицательны. Значит, нужно сравнить их модули. У второго числа модуль больше, значит, само число меньше.

Сначала сравним модули этих чисел:
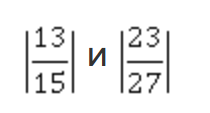
Разложим на множители оба знаменателя. Общий знаменатель – это три тройки и одна пятерка. Домножим у первой дроби числитель и знаменатель на две тройки, а у второй – на 5.
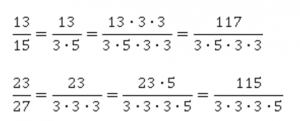
Получаем две дроби с одинаковыми знаменателями. Считать их не будем. Но числитель первой дроби больше второго.
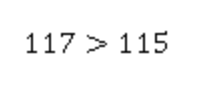
Первая дробь больше.
Значит:
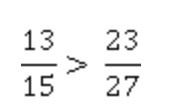
И тогда:
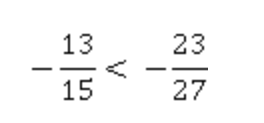
Заключение
Итак, подведем итог.
- Отрицательные числа появляются как инструмент, упрощающий вычисления.
- Договоренность про сравнение этих чисел следующая:
- Любое отрицательное число меньше любого положительного.
- Ноль находится между всеми отрицательными и всеми положительными числами (больше любого отрицательного и меньше любого положительного).
- Из двух отрицательных чисел больше то, у которого меньше модуль.
- Кроме того, что отрицательные числа упрощают вычисления, в обычной жизни им тоже нашли применение. Например, для упорядочивания, для обозначения температуры по шкале Цельсия, этажей ниже первого.
Список литературы
- Виленкин Н. Я. Жохов В. И. Чесноков А. С. Шварцбурд С. И. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А. Г., Полонский В. В., Якир М. С. Математика 6 класс. – Гимназия, 2006.
- Депман И. Я., Виленкин Н. Я. За страницами учебника математики. – М.: Просвещение, 1989.
- Рурукин А. Н., Чайковский И. В. Задания по курсу математика 5-6 класс. – ЗШ МИФИ, 2011.
- Рурукин А. Н., Сочилов С. В., Чайковский К. Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
- Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. Математика: учебник-собеседник для 5-6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «matematika-na.ru» (Источник)
Домашнее задание
- Виленкин Н. Я., Жохов В. И., Чесноков А. С. и др. Математика 6. – М.: Мнемозина, 2012 (ссылка см. 1.2).
- Домашнее задание: № 976, № 981, № 996.
- Другие задания: № 980, № 998, № 1000.
Оцените урок:




