Деление
На этом уроке мы поговорим о делении чисел с разными знаками, а также о делении отрицательных чисел. Кроме того, разберём несколько примеров.
Введение
Деление на положительное число эквивалентно умножению на обратное ему число. Например,![]() .
.
Но у любого отрицательного числа тоже есть обратное. И деление на отрицательное число тоже можно заменить умножением на обратное: ![]()
Давайте вспомним определение. Два числа называются взаимно обратными, если их произведение равное единице: если ![]() – взаимно обратные числа.
– взаимно обратные числа.
Но это значит, что взаимно обратные числа всегда имеют один и тот же знак. Если бы они были разных знаков, то их произведение получилось бы отрицательным.
Правила деления
Отрицательное число можно представить как произведение -1 на противоположное положительное число: ![]() . Этот факт и позволяет получить правила умножения чисел с разными знаками. Например:
. Этот факт и позволяет получить правила умножения чисел с разными знаками. Например: ![]() Но при делении получается такая же ситуация:
Но при делении получается такая же ситуация: ![]()
То есть правило деления чисел с разными знаками аналогично правилу умножения. Их даже можно объединить в одно правило: выполнять умножение или деление двух чисел нужно, не обращая внимания на знаки. Если числа были одного знака, то результат будет положительным, а если разного – то отрицательным.
Примеры
![]()
Делим, не обращая внимания на знак. Так как числа разных знаков, то в ответе ставим минус:
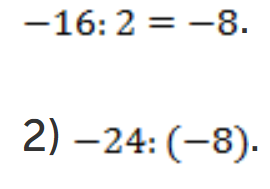 .
.
Делим 24 на 8, так как числа оба отрицательные, то ответ положительный:
![]()
![]()
Делим 1,8 на 3, так как знаки у чисел разные, в ответе минус: ![]() .
.
Часто, чтобы понять, какой знак получится, правило запоминают так: «минус на минус дает плюс, плюс на минус дает минус». Это верно и для умножения и для деления.
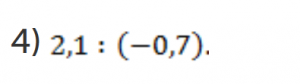
Делимое и делитель можно умножить на 10. Так как числа разных знаков, то в ответе ставим минус:
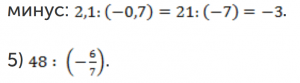
Знак ответа минус, его можно сразу поставить впереди, т.к. у чисел разные знаки. Деление заменяем умножением. Сокращаем и получаем ответ:
![]()
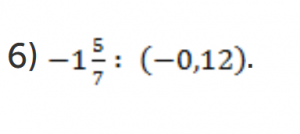
Сразу определяем знак. Минус на минус дают плюс. Запишем смешанную дробь в виде неправильной и сократим на 12, деление на 0,,01 означает умножение на 100. Выделяем целую часть и получаем ответ: ![]()
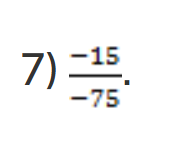
Дробь – это тоже деление. Минус на минус дают плюс. Сокращаем дробь на 5 и на 3. Можно записать в виде десятичной дроби: ![]() .
.
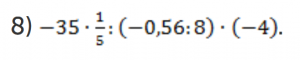
Если в выражении несколько операций умножения и деления, то правило то же самое. Два первых минуса дают плюс. Остается один. В ответе минус. Или так: всего три минуса. Нечетное количество минусов дает минус: ![]()
Заключение
Деление можно считать умножением. Поэтому правило умножения чисел с разными знаками подходит и для деления. Заключается правило в следующем: чтобы выполнить действия с несколькими умножениями и делениями, нужно выполнить действия, не обращая внимания на знаки. Четное количество минусов в исходном выражении даст плюс в ответе, нечетное – минус.
Если мы умножаем всего два числа или делим одно число на другое, то правило звучит проще: минус на минус дает плюс, плюс на минус дает минус.
Тот факт, что деление можно заменить умножением на обратное число, мы использовали, чтобы объяснить, почему правило умножения подходит и для деления.
При расчетах такую замену делать совсем не обязательно. Все зависит от конкретного примера. В примере ![]() это в самом деле удобно сделать:
это в самом деле удобно сделать: ![]() . А в примере
. А в примере ![]() , если заменить деление умножением, то удобнее не станет, поэтому считаем так, как есть:
, если заменить деление умножением, то удобнее не станет, поэтому считаем так, как есть: ![]() .
.
Список рекомендованной литературы
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. – М.: «Просвещение», 2010.
- Виленкин Н.Я. и др. Математика. Учебник для 6 класса. – М.: ИОЦ «Мнемозина», 2013.
Дополнительные рекомендованные интернет-ресурсы
- Интернет-портал «math-prosto.ru» (Источник).
- Интернет-портал «mathematics-repetition.com» (Источник).
Домашнее задание
Пожалуйста, выполните указанные задания.
- Определите знак частного:
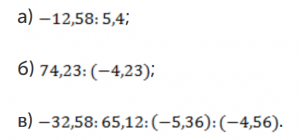
- Выполните деление:
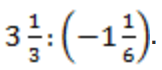 .
.
Найдите значение выражения: ![]()
Оцените урок:
До 2030 года: исчезнут 67 профессий и появятся новых 186 🤖
Посмотреть в Telegram



