На этом уроке вы узнаете, в каких случаях удобно применять положительные и отрицательные числа для обозначения изменений различных величин.

Если у вас возникнут трудности с пониманием темы, мы рекомендуем ознакомиться с уроками «Измерение» и «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур».

Введение
Изменение величины можно обозначать с помощью положительных и отрицательных чисел. Например, увеличение величины можно представить как положительное число, а уменьшение – как отрицательное (см. Рис. 1).

Рис. 1. 

Мы далеко не всегда так поступаем. В самом деле редко кто скажет: «Изменение температуры составило+3 °C или-3°C». Обычно мы говорим: «Температура повысилась на  градуса или понизилась на 3 градуса».

Так когда все-таки удобно использовать положительные и отрицательные числа для обозначения изменения различных величин?

Пример 1. Учет на складе

Предположим, что мы выдаем мячи на спортивном складе: люди приходят к нам и отдают мячи либо забирают. В начале рабочего дня мы пересчитываем мячи. Например, их оказалось 85 штук. Количество выданных мячей мы обозначаем отрицательным числом, принятых обратно – положительным (Рис. 2).

Рис. 2. Удобства записи

Удобство такой записи в том, что мы в любой момент можем посчитать, сколько мячей в данный момент на складе, не пересчитывая каждый раз общее количество. Считаем общее движение мячей: . Значит, общее количество уменьшилось на 8 и сейчас на складе 77 мячей (Рис. 3).

Рис. 3. Общее количество мячей на складе после всех движений мячей

Итак, запись изменения величины с помощью положительных и отрицательных чисел удобна, когда нам нужно знать в любой момент эту величину, непосредственно ее не измеряя (например, не пересчитывая общее количество мячей).

Пример 2. Денежные расчеты

Задача взаимных расчетов похожа на задачу с мячами. Но есть и отличие. Когда мы звоним по телефону – тратим деньги со счета или зачисляем деньги на счет, то нет такого места, где лежали бы купюры или монеты, которые можно пересчитать. Таким образом, учет потраченных и зачисленных средств – единственный способ знать в каждый момент, сколько денег на счете. Ну а сам способ расчета точно такой же, как в предыдущем примере. Зная начальную сумму на счете (например, 30 рублей), обозначая потраченные средства отрицательным числом, а зачисленные – положительным, всегда легко узнать, сколько денег на счете в данный момент. Более того, мы можем даже поговорить в долг, то есть в какой-то момент на счету может быть отрицательное количество денег (Рис. 4).

Рис. 4. Изменение количества денег на счете

Итак, запись изменения величины с помощью положительных и отрицательных чисел удобна, когда сама величина виртуальна, не имеет физического носителя (как счет на мобильном телефоне).

Пример 3. Движение по прямой

Перемещение в физике определяют как разность между координатами конечной и начальной точек. Если координата точки после перемещения стала больше, то перемещение положительное, а если меньше, то отрицательное (Рис. 5).

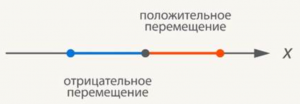
Рис. 5. Положительное и отрицательное перемещение

Например, перемещение из точки 0 в точку 7 равно 7, а из точки 7 в точку 3 равно -4 (Рис. 6).

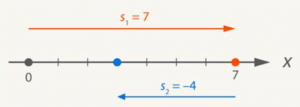
Рис. 6. Иллюстрация к примеру

Пример 4. Отслеживание динамики

Иногда важнее знать, не чему равна величина после нескольких ее изменений, а чему именно равно изменение и в какую сторону оно происходило. Например, для акций компаний часто самой важной информацией является не цена акций, а как эта цена менялась в последнее время, дешевели или дорожали акции и насколько. Изменения цен на акции записывают с помощью положительных и отрицательных чисел. И уже на основе этих данных принимаются решения, продавать или покупать акции. Или делаются выводы, хорошо или плохо идут дела в самой компании (Рис. 7).

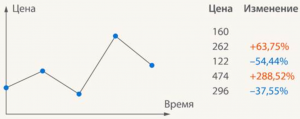
Рис. 7. Изменения цен в процентах

Заключение
Таким образом, ключевая идея урока заключается в том, что изменения величин часто обозначаются с помощью положительных и отрицательных чисел. Это не только упрощает вычисления, но и делает их более наглядными. Если же в конкретной задаче использование этого инструмента (положительных и отрицательных чисел) не приносит упрощения, то его можно и не применять.

Список рекомендуемой литературы

• Зубарева И.И., Мордкович А.Г. «Математика. 6 класс». М.: ИОЦ «Мнемозина», 2014.
• Дорофеев Г.В., Петерсон Л.Г. «Математика. 6 класс. Учебник в 3 частях». М., 2010.
• Виленкин Н.Я. и др. «Математика. Учебник для 6 класса». М.: ИОЦ «Мнемозина».

Дополнительные ресурсы в интернете

• Интернет-портал «urok.1sept.ru»
• Интернет-портал «school-assistant.ru»
• Интернет-портал «videouroki.net»

Домашнее задание

1. Длина пружины в состоянии покоя составляет мм. Какова длина пружины, если она:
   А) увеличилась на мм,
   Б) уменьшилась на мм,
   В) уменьшилась на мм,
   Г) увеличилась на мм?

2. Заполните пропуски: .

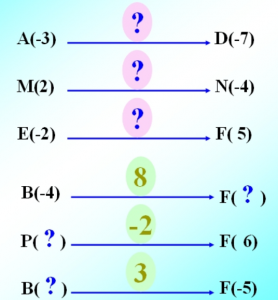
3. Какое давление в колесе автомобиля, если утром оно было 2 атмосферы, а в течение дня менялось: А) на -0,3 атмосферы; Б) на 0,1 атмосферы; В) на -0,4 атмосферы; Г) на -0,9 атмосферы.