Сложение чисел с помощью координатной прямой
На этом уроке мы поговорим, как можно облегчить и визуализировать сложение чисел, используя координатную прямую.
Введение
Если маленькому ребёнку показать две машинки в одной комнате, он их посчитает: 1, 2 (Рис. 1.).
Рис. 1. Две машинки в одной комнате
Если теперь показать ему три машинки в другой комнате, их он тоже без проблем посчитает: 1, 2 ,3 (Рис. 2.).
Рис. 2. Три машинки в другой комнате
А если теперь спросить, сколько всего машинок в двух комнатах, то он, скорее всего, попытается их перенести в одну комнату и посчитать: 
(Рис. 3).
Рис. 3. Пять машинок в одной комнате
Это пример предметного счёта.
Мы же справимся быстрее, поскольку знаем, что 2 + 3 = 5, независимо от того, что мы складываем: машинки, дома, орехи, шаги. И независимо от того, где они находятся друг относительно друга.
Человечество когда-то совершило этот переход, и каждый из нас проходит подобный путь. Постепенно, незаметно для себя, мы отходим от предметного счета и начинаем считать более абстрактно. Однако иногда люди возвращаются к предметному счету, что может показаться шагом назад. Для чего это может быть необходимо? Существует два основных варианта:
- Когда нужно пересчитать конкретные предметы, например, количество книг на полке или количество шагов от дома до дерева.
- Чтобы лучше понять, откуда берутся правила, которые мы применяем; иногда полезно вернуться к предметному счету, чтобы осознать, почему правила устроены именно так.
Сегодня мы обсудим сложение чисел с точки зрения предметного счета, используя точки на числовой прямой в качестве нашего объекта. Это более удобно, чем работать с другими предметами, и нам понадобится только бумага и ручка.
Кроме того, мы должны научиться связывать точки в пространстве с числами. Эта концепция будет полезна не только для решения математических задач, но и, например, в физике, которую вы начнете изучать в будущем.
Сложение положительных чисел с помощью координатной прямой
Для начала давайте обсудим правило, которое мы давно знаем: от перестановки слагаемых сумма не изменяется. Мы настолько привыкли к этому, что даже не задумываемся: а почему так? Что такое 5 + 3? Это от нуля пять шагов, а потом еще три шага. Всего 8 (Рис. 4).
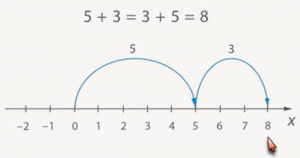
Рис. 4.
Но ведь можно посчитать и в обратную сторону. И это уже 3 + 5 = 8 (Рис. 5).
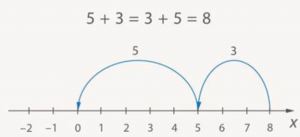
Рис. 5. Верно и в обратную сторону
Но расстояние, количество шагов, одно и то же. И это верно для суммы любых двух чисел.
Сложение чисел разных знаков с помощью координатной прямой
Мы говорили о том, что отрицательные числа вводились таким образом, чтобы они подчинялись тем же правилам (законам), что и положительные числа. Давайте убедимся, что для отрицательных чисел сумма также не будет меняться при перестановке.
Каждое число состоит из знака и модуля. Знак показывает, в какую сторону нужно двигаться, а модуль – на сколько единиц. Начинаем отсчет от 0. Например, убедимся, что 3 — 7 = -7 + 3. Посчитаем с помощью координатной прямой значение и того, и другого выражений.
3 — 7 = -7 + 3
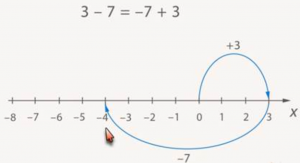
Рис. 6.
Рис. 7.
Примеры
Рассмотрим ещё несколько примеров.
1. Чему равна разность 2 — 5 = ?
Первое число 2. Знак перед ним не стоит, значит, подразумевается плюс, движение вправо. От нуля движемся вправо на 2 единицы. От точки 2 переходим влево на 5 единиц. Приходим в точку 
(Рис. 8).
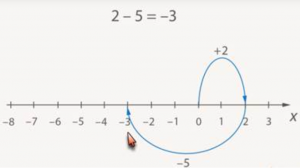
Рис. 8.
2. Чему равна разность — 3 — 4 = ?
-3 значит, что движемся от нуля влево на 3. От точки -3 движемся влево на 4 единицы. Получаем точку 
(Рис. 9).
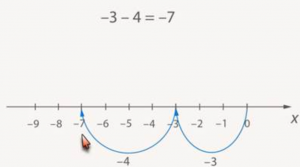
Рис. 9.
Задание
Найти значение выражений.
1. -2 + 4
Движемся от нуля влево на 2 шага, а затем от -2 вправо на 4 шага. Приходим в точку 2 (Рис. 10).
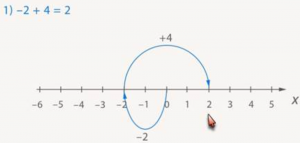
Рис. 10.
2. — 4 — 5
Начинаем от нуля. Движемся влево на 4 единицы, а затем от -4 еще на 
единиц влево. Приходим в точку -9 (Рис. 11).
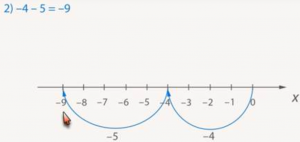
Рис. 11.
3. 4 — 3 — 3
Начинаем от нуля. Двигаемся вправо на 4 шага, затем влево на 3 шага, и еще раз влево на 3 шага. Приходим в точку -2 (Рис. 12).
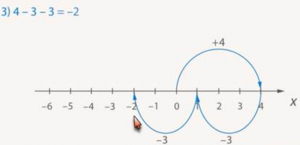
Рис. 12.
4. -4 + 4
Начинаем от нуля. Движемся влево на 4 шага, затем вправо на 4 шага. Приходим в точку 0 (Рис. 13).
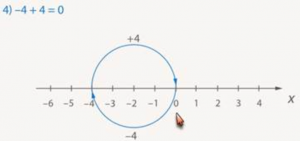
Рис. 13.
5. 
Так как x > 0, то сначала сдвигаемся вправо на x единиц, потом влево на x единиц. Приходим в точку 0 (Рис. 14).
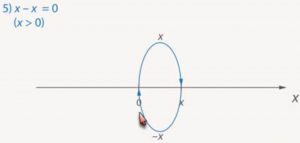
Рис. 14.
6. 
Первый шаг от нуля – влево (так как x < 0). Противоположное число — x, является положительным. Прибавить — x означает сдвиг вправо на положительное число -x. Приходим в точку 0 (Рис. 15).
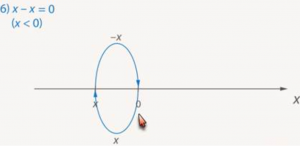
Рис. 15.
Получили, что разность x — x = 0 всегда, не зависимо от того, положительное число 
или отрицательное (Рис. 16).
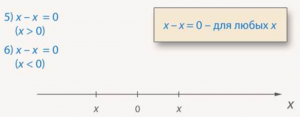
Рис. 16.
Заключение
Таким образом, числовая прямая служит инструментом для возвращения к предметному счету, где точки выступают в роли объектов. Этот подход позволяет нам лучше понять основные свойства арифметических операций. Например, мы можем увидеть, что перестановочное свойство справедливо для всех чисел, а не только для положительных. Тем не менее, использование числовой прямой как вспомогательного средства при сложении не является необходимым, поскольку правила алгебраического сложения достаточно просты и не требуют дополнительных инструментов. Научению этим правилам мы посвятим наши следующие занятия.
Список рекомендуемой литературы
- Зубарева И.И., Мордкович А.Г. «Математика. 6 класс». М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. «Математика. 6 класс. Учебник в 3 частях». М.: «Просвещение», 2-е изд., перераб. — 2010; Ч.2.
- Виленкин Н.Я. и др. «Математика. Учебник для 6 класса». М.: ИОЦ «Мнемозина», 2013.
Дополнительные рекомендованные интернет-ресурсы
- Интернет-портал «school-assistant.ru»
- Интернет-портал «mathematics-repetition.com»
- Интернет-портал «cleverstudents.ru»
Домашнее задание
- На какой координатной прямой (Рис. 1) правильно выполнено действие 5 — 7 ?
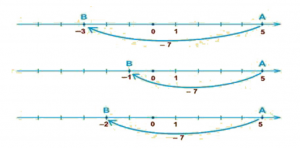
2. С помощью координатной прямой найдите сумму чисел: а) 5 + 6; б) 4 — 9; в) -2 -13; г) 5 -5.
3. С помощью координатной прямой найдите сумму чисел: а) 3 — 5 + 7; б) 6 + 4 — 4; в) -3 — 14 + 15; г) -5 + 9.
Оцените урок:
