Случай 1

Давайте рассмотрим такой пример:

Схема 1

Решение: 1. Попробуйте нарисовать цифру 1 и перенести на нее все необходимые данные.

На рисунке 1 видно, что остался всего 1 квадрат.

Давайте разбьем первый пример «на столбцы». Когда мы делим 7 на 2, мы берем по 3 в каждом. Как вы можете видеть как из схемы 1, так и из решения столбца, остальное равно 1.

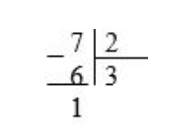
Схема 2

2. Выполним деление для следующего примера с помощью схемы 2 и деления «в столбик».

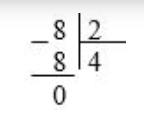
Как видно, деление выполнено без остатка.

3. Разделим пример в (схема 3).

Схема 3

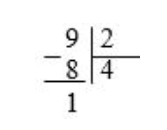
В результате деления остаток – 1.

4. Разделим пример г (схема 4).

Схема 4

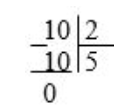
Десять на два поделилось без остатка.

Примеры № 2

Решите данные примеры, выполните рисунки и заполните таблицу 1.

а) 6:3                                  

б) 7:3                                 

в) 8:3                       

г) 9:3

Решение: 1. Разделим шесть на три (схема 5).

Схема 5

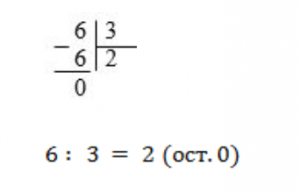
2. Разделим семь на три (схема 6) 

Схема 6

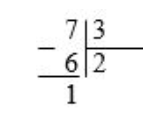
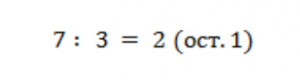
3. Разделим восемь на три (схема 7)

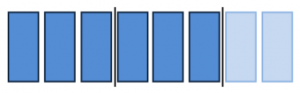
Схема 7

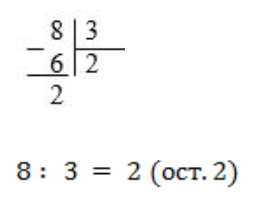
4. Разделим девять на три (схема 8)

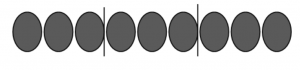
Схема 8

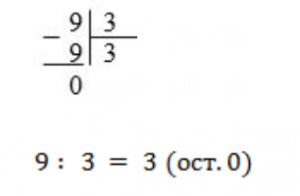
5. Используя полученные данные, заполним таблицу 1.

Таблица 1. Примеры № 2

Проанализируем данные таблицы 1, и увидим, что остаток не может быть больше, чем делитель.

Задания № 1

Остатки при делении

1. Остатки при делении на 4
   При делении любого числа на 4 возможные остатки должны быть меньше делителя. Таким образом, при делении на 4 могут возникать остатки: 0, 1, 2 и 3.

2. Остатки при делении на 5
   При делении на 5 остаток также не может превышать делитель. Следовательно, возможные остатки при делении на 5: 0, 1, 2, 3 и 4.

3. Остатки при делении на 7
   При делении любого числа на 7 остаток будет меньше 7. Поэтому возможные остатки будут: 0, 1, 2, 3, 4, 5 и 6.

Правила деления с остатком

Деление с остатком можно выполнять без использования схем и рисунков, если придерживаться определённых правил (см. схема 9).

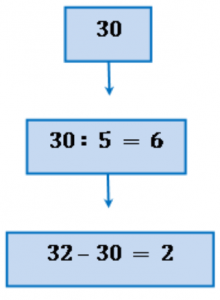
Рассмотрим пример деления 32 на 5.

Решение:

1. Найдём ближайшее к 32 число, которое делится на 5 без остатка. Это число – 30. Разделив 30 на 5, мы получим частное 6. Затем из 32 вычтем 30, чтобы найти остаток.

Частное
Остаток
Схема 9

Способ подбора

Иногда при делении с остатком бывает трудно выбрать самый большой делитель, тогда решают пример методом подбора.

Например, 34 : 9 можно делить так. Предполагаем любой ответ. Проверяем умножением. Остаток сравниваем с делителем:

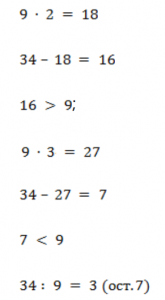
Примеры № 3

Выполните деление с остатком методом подбора.

а) 25:10                  б) 53:8

Решение: 1. Для решения первого примера попробуем цифру 2:

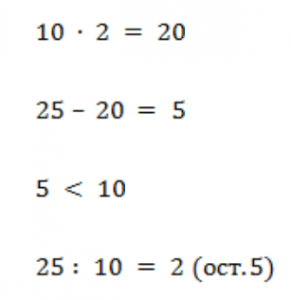
2. Решим второй пример по изученному алгоритму. Помним о том, что остаток должен быть всегда меньше делителя. Делитель можно подбирать несколько раз:

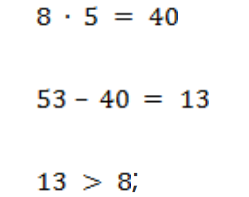
Остаток (13) больше делителя (5) для примера б – необходимо продолжать увеличивать делитель.

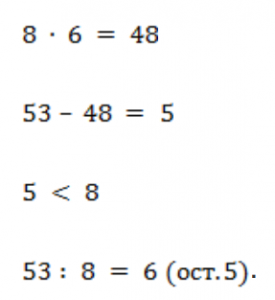
Список литературы

1. Математика. 3 класс. Учебное пособие для общеобразовательных учреждений с приложением на электронных носителях. В 2 частях. Часть 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 2-е издание. – Москва: Просвещение, 2012. – 112 страниц: иллюстрации. – (Школа России).

2. Рудницкая, В. Н., Юдачёва, Т. В. Математика, 3 класс. – Москва: ВЕНТАНА-ГРАФ.

3. Петерсон, Л. Г. Математика, 3 класс. – Москва: Ювента.

Дополнительные рекомендованные интернет-ресурсы

1. Интернет-портал «math-prosto.ru» (Источник)
2. Интернет-портал «cleverstudents.ru» (Источник)
3. Интернет-портал «shkolo.ru» (Источник)

Домашнее задание

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 26 № 1–3.
2. Вычисли с помощью рисунков и в столбик.
   
3. Реши методом подбора:
4.                  
5. ^* Объясни, почему при делении любого числа на 8, остаток может быть только: 0, 1, 2, 3, 4, 5, 6, 7.