Решение задачи с кружками

На рисунке слева изображены два желтых кружка, справа – один белый.

Найдем, сколько всего кружков изображено. Для этого к двум желтым кружкам прибавим один белый.

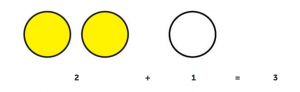
Получаем три кружка.

Далее поменяем кружки местами. Белый кружок переместим и поставим слева, а два желтых будут справа. Изменилось ли количество кружков?

Запишем, какое действие необходимо выполнить. Для этого к одному белому прибавим два желтых.

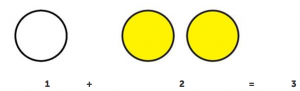
Вы можете видеть, что количество кружочков осталось прежним.

Решаем задачу с квадратиками

Проделываем то же действие в квадрате. Добавляем 3 розовых квадратика к 2 зеленым и записываем, какое действие получилось.

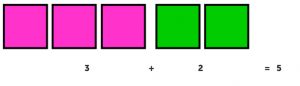
Получилось 5 квадратов.

Теперь поменяем местами зеленые и розовые квадраты. К двум зеленым добавим три розовых квадрата.

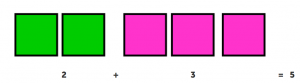
Количество квадратиков не изменилось. Их всего 5.

Дополнительные действия, цифры при добавлении

Давайте вспомним, какие действия мы всегда выполняли. Действие добавления было выполнено. Теперь давайте вспомним, что число при сложении называется суммой и значением суммы.

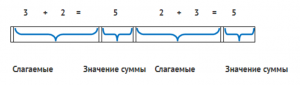
Формулировка переместительного свойства сложения

Что мы делали с кругами и квадратами? Мы меняли их местами. Таким образом, мы доказали, что при перестановке слагаемых сумма остается неизменной. В математике это известно как переместительное свойство сложения.

Пример использования переместительного свойства сложения

Пример 1.

На иллюстрации представлены два столбика с примерами. Необходимо найти суммы в левом и правом столбиках, которые имеют одинаковое значение, и соединить их стрелочками.

Правильный ответ:

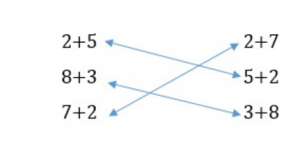
То есть, не нужно выполнять вычисления, чтобы найти суммы с одинаковым значением, поскольку можно воспользоваться переместительным свойством сложения.

Мы знаем, что переместительное свойство сложения – это когда слагаемые меняются местами.

2 + 5 =  7                                       5 + 2 = 7

От перестановки слагаемых сумма не меняется.

Примените переводимость сложения для решения уравнения

Пример 2.

Вам нужно добавить уравнение, используя характеристики перевода терминов.

1 + 2 = 2 + …

8 + 2 = … + …

6 + 4 = … + …

7 + 3 = 4 + 6

Для этого достаточно поменять слагаемые местами.

Правильный ответ:

1 + 2 = 2 + 1

8 + 2 = 2 + 8

6 + 4 = 4 + 6

Тут мы применили переместительное свойство сложения. Теперь давайте подумаем, подходит ли равенство 7 + 3 = 4 + 6 для нашего задания?

Правильный ответ: нет. Хотя обе суммы равны (7 + 3 = 10 и 4 + 6 = 10), это равенство не иллюстрирует перемещение слагаемых, а значит, мы не использовали переместительное свойство сложения.

Таким образом, на сегодняшнем уроке мы изучили переместительное свойство сложения, которое утверждает, что изменение порядка слагаемых не влияет на итоговую сумму. Также мы повторили, как называются числа, участвующие в сложении.

Список литературы

1. Александрова Л. А., Мордкович А. Г. Математика 1 класс. – М.: Мнемозина, 2012.
2. Башмаков М. И., Нефедова М. Г. Математика. 1 класс. – М.: Астрель, 2012.
3. Беденко М. В. Математика. 1 класс. – М.: Русское слово, 2012.

Дополнительные рекомендованные ресурсы в Интернете

• Законы арифметики (Источник)
• Фестиваль педагогических наук «Открытый урок» (Источник)
• Интернет-портал «infourok.ru» (Источник)

Домашнее задание

Какое основное правило переместительного свойства сложения?

Запишите выражения, пользуясь переместительным свойством сложения:

4 + 2 = ?

6 + 3 = ?

1 + 7 = ?

5 + 9 = ?    

Как называются числа при сложении?