Примеры № 1

А. Найдите значение, соблюдая порядок действий:

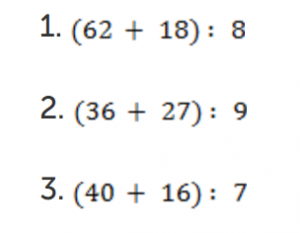
Решение: 1. Для первого примера найдём сумму. Далее разделим результат на число 8:

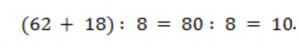
2. Вычислим сумму в скобках для второго примера. Потом разделим результат на девять:

3. По такому же алгоритму решим третий пример:

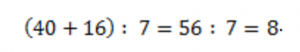
B.To к какому из этих выражений я могу применить правило для деления суммы на число?

Решение: 1. Если внимательно посмотреть на 2-й пример, то можно увидеть, что именно к нему можно применить правило деления суммы на число. Чтобы разделить сумму на число, вам нужно разделить каждый член на это число и сложить полученное частное.

Примеры № 2

Сравните пары выражений: 

Решение: 1. Если вы анализируете пары в примере, обратите внимание, что делители каждой пары одинаковы, но сами делители разные. Чтобы найти значение, вам нужно применить правило, которое заменяет делимый член парой слагаемых и делит сумму на число. Обратите внимание, что слагаемое должно быть разделено на этот делитель:

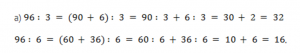
2. Каждый раз учитываем то, что слагаемые можно подобрать так, чтобы они легко делились на делитель:

3. Проделаем аналогичную операцию и для третьей группы примеров:

4. После того как мы написали ход решения каждого примера, сравним это примеры и увидим, что в одну группу попадут выражения, в которых делимое заменено разрядными слагаемыми, а в другую такие, у которых удобные слагаемые:  

Если в делимом число единиц меньше, чем делитель, то это делимое можно заменить только удобными слагаемыми.

Примеры № 3

Замените делимое удобными слагаемыми и решите примеры (рис. 1).

1. 72 : 3

2. 72 : 4

3. 72 : 6

Рис. 1. Примеры

Решение: 1. В первом примере, в числе 72, у нас есть две единицы, которые меньше делителя 3, поэтому нам нужно заменить весь делитель суммой удобных слагаемых:

2. Аналогично анализируем второй пример:

3. В третьем примере в делимом на месте единиц число меньше, чем делитель, поэтому данное делимое заменим на сумму удобных слагаемых:

Задание № 1

Разгадайте правило, по которому составлены схемы 1–3, и впишите недостающие числа.

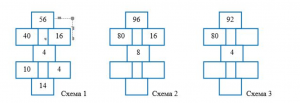
Решение: 1. Проанализируем схему 1. Число 56 будем делить на 4, поэтому раскладываем его на слагаемые, а полученные результаты прибавляем:

2. По такому принципу поступим и со второй схемой:

Теперь данная схема приобретёт следующий вид (схема 4):

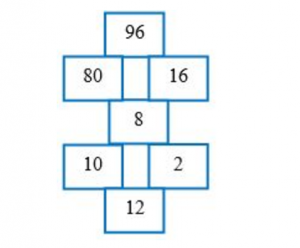
3. По данному правилу допишем недостающие числа в схеме 3:

Так схема 3 будет иметь вид (схема 5):

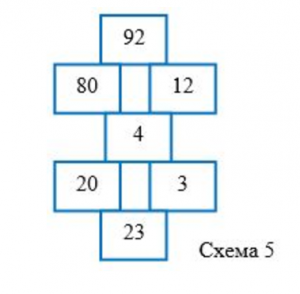
Список литературы

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России). 
2. Рудницкая В. Н., Юдачёва Т. В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
3. Петерсон Л. Г. Математика, 3 класс. – М.: Ювента.

Домашнее задание

1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 2 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 5 № 7, ст. 9 № 2, 4.
2. Каждый пример реши двумя способами:
3. 
4. Два мешка картошки по 80 кг поместили в ящики по 4 кг в каждом. Сколько ящиков потребовалось?
5. ^* 108 кг винограда расфасовали в корзины по 2 кг в каждую. А помидоры количеством 99 кг – по 9 кг в ящик. Известно, что огурцов было в два раза больше, чем помидоров, и их также расфасовали по 9 кг в ящик. Сколько ящиков и корзин потребовалось?