Равные множества
Равенство множеств
Важное понятие в теории множеств. Множества называются равными, если они содержат одинаковые элементы, независимо от порядка их расположения.
Предположим, у нас есть два множества. Рассмотрим их на примере (рис. 1).

Рис. 1. Иллюстрация к примеру
В одной руке – два карандаша, а в другой – три. Равны ли множества? Нет, не равны, потому что в них разное количество элементов (рис. 2).
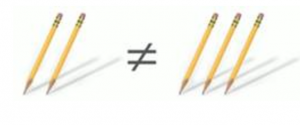
Рис. 2. Иллюстрация к примеру
Другой пример: в одной руке – два карандаша, а в другой – карандаш и ручка (рис. 3).

Рис. 3. Иллюстрация к примеру
Равны ли множества теперь? В математике такие множества не равны, потому что предметы в множествах разные, одинаково только количество (рис. 4).
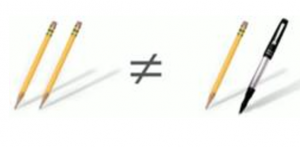
Рис. 4. Иллюстрация к примеру
Третий пример: в одной руке два карандаша, и в другой два карандаша (рис. 5).
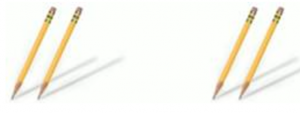
Рис. 5. Иллюстрация к примеру
Равны ли множества теперь? Да, равны (рис. 6).
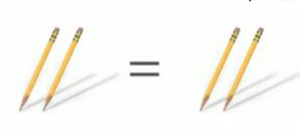
Рис. 6. Иллюстрация к примеру
Сделаем вывод: равными называются множества, состоящие из одинакового числа одинаковых элементов (рис. 7).

Рис. 7. Определение
Рассмотрение примеров
Рассмотрим пример (рис. 8):

Рис. 8. Иллюстрация к примеру
Сравним элементы двух множеств. В первом множестве есть паровозик, во втором тоже есть. В первом множестве есть юла, во втором тоже есть. В первом множестве есть мишка, во втором тоже. В первом множестве – машинка, а во втором – лягушонок.
Делаем вывод: элементы множеств разные.
Из этого следует, что множества не равны (рис. 9).

Рис. 9. Иллюстрация к примеру
Рассмотрим второй пример (рис. 10).

Рис. 10. Иллюстрация к примеру
Сравним множества. В первом множестве – три вишни, во втором – тоже три вишни. В первом множестве – две ягоды малины, во втором множестве – тоже две ягоды. В первом множестве – одна клубника, во втором – тоже одна.
Делаем вывод: элементы множеств одинаковые. Количество элементов в множествах одинаковое. Значит, множества равны (рис. 11).

Рис. 11. Иллюстрация к примеру
Рассмотрим третий пример (рис. 12).
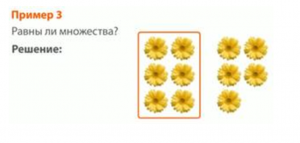
Рис. 12. Иллюстрация к примеру
В двух множествах одинаковые желтые цветы. В первом множестве – 6 цветков, во втором – пять.
Вывод: элементы множеств одинаковые. Количество элементов в множествах разное. Значит, множества не равны (рис. 13).

Рис. 13. Иллюстрация к примеру
Подведем итог: множества будут равными, если они состоят из одинакового количества одинаковых элементов (рис. 14).

Рис. 14. Определение
Закрепление материала
Давайте применим полученные знания на практике.
Задача 1: определим множество, равное данному.
Первое множество отличается по цвету. Второе — по количеству элементов. Третье множество является равным исходному (рис. 15).

Рис. 15. Иллюстрация к задаче
Задача 2: уравняем множества, убрав лишний элемент (рис. 16).

Рис. 16. Иллюстрация к задаче
Сравним множества. Лишний элемент в первом множестве – тарелка. Уберем её и получим равные множества (рис. 17).

Рис. 17. Иллюстрация к задаче
Задача 3: уравняем множества, добавив элемент (рис. 18).

Рис. 18. Иллюстрация к задаче
В первое множество следует добавить кленовый лист. Теперь множества равны (рис. 19).

Рис. 19. Иллюстрация к задаче
Сделаем вывод: чтобы уравнять множества, добавьте недостающий элемент или уберите лишний (рис. 20).

Рис. 20. Правило
Задача 4: найдем равные множества (рис. 21).

Рис. 21. Иллюстрация к задаче
Сравним множества и определим, что множества 1 и 4, а также 3 и 6 равны.
Итоги урока
Подведем итог урока: множества считаются равными, если они содержат одинаковое количество одинаковых элементов.
Список литературы
Александрова Л. А., Мордкович А. Г. Математика. 1 класс. – М: Мнемозина, 2012.
Башмаков М. И., Нефёдова М. Г. Математика. 1 класс. – М: Астрель, 2012.
Беденко М. В. Математика. 1 класс. – М.: Русское слово, 2012.
Дополнительные рекомендованные ресурсы
Интернет-ресурс «myshared.ru» (Источник)
Домашнее задание
- Какие множества называются равными?
- Какими способами можно уравнять множества?
- Нарисуйте картинку-задачу на поиск равных множеств.
Оцените урок:




