Главная > Решение задач на встречное движение
Решение задач на встречное движение
Введение
Вы уже знакомы с понятием «средняя скорость» и понимаете, как взаимосвязаны такие величины, как скорость, время и расстояние. Давайте разберем более сложные задачи.
Задача 1 (Способ 1)
Два лыжника одновременно вышли навстречу друг другу из двух поселков и встретились через 3 часа. Первый лыжник двигался со средней скоростью 12 км/ч, а второй – 14 км/ч. Необходимо определить расстояние между поселками. Смотрите иллюстрацию на рисунке 1.
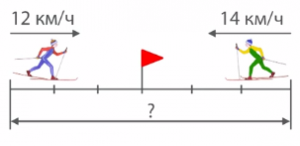
Рис. 1. Иллюстрация к задаче 1
Решение
Способ 1
Чтобы найти расстояние между поселками, нужно определить, какое расстояние прошел каждый лыжник. Для этого необходимо знать их среднюю скорость и время в пути.
Лыжники двигались 3 часа. Следовательно, каждый из них был в пути 3 часа.
Для первого лыжника: средняя скорость 12 км/ч, время 3 часа. Рассчитаем расстояние, которое он прошел:
Для второго лыжника: средняя скорость 14 км/ч, время в пути также 3 часа. Рассчитаем расстояние, которое он прошел:
Теперь находим общее расстояние между поселками:
Ответ: Расстояние между поселками составляет 78 км.
Способ 2
За первый час первый лыжник прошел 12 км, а второй лыжник – 14 км. Найдем скорость сближения:
Таким образом, за 3 часа лыжники сблизились на:
Ответ: Расстояние между поселками составляет 78 км.
Задача 2
Из двух поселков, расстояние между которыми равно 78 км, одновременно вышли навстречу друг другу два лыжника. Первый лыжник двигался со средней скоростью 12 км/ч, а второй – 14 км/ч. Через сколько часов они встретятся? (Смотрите рисунок 2).
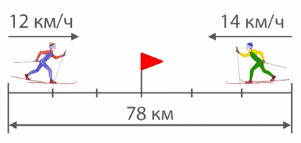
Рис. 2. Иллюстрация к задаче 2
Чтобы определить время встречи лыжников, необходимо знать их скорости и общее расстояние.
Первый лыжник приближается к месту встречи на 12 км за час, а второй – на 14 км. Совместно они сближаются на:
Теперь, зная общее расстояние и скорость сближения, можно вычислить время до встречи:
Ответ: Лыжники встретятся через 3 часа.
Задача 3
Из двух поселков, расстояние между которыми составляет 78 км, одновременно вышли навстречу друг другу два лыжника и встретились через 3 часа. Первый лыжник шел со средней скоростью 12 км/ч. Определите среднюю скорость второго лыжника. (Смотрите рисунок 3).
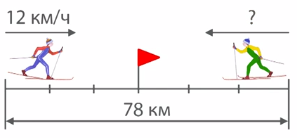
Рис. 3. Иллюстрация к задаче 3
Решение
Чтобы вычислить среднюю скорость второго лыжника, необходимо определить, какое расстояние он прошел до встречи и сколько времени был в пути. Общее расстояние, которое прошли оба лыжника, равно 78 км. Сначала найдем расстояние, которое прошел первый лыжник:
Теперь можем вычислить, какое расстояние прошел второй лыжник:
Теперь, зная расстояние, которое прошел второй лыжник, и время в пути (3 часа), найдем его среднюю скорость:
Ответ: Средняя скорость второго лыжника составляет 14 км/ч.
Заключение
Сегодня мы изучили, как решать задачи на встречное движение.
Список литературы
- Математика. Учебник для 4 кл. нач. школы. В 2 ч. / М. И. Моро, М. А. Бантова. – М.: Просвещение, 2010.
- Демидова Т. Е., Козлова С. А., Тонких А. П. Математика. 4 класс. Учебник в 3 ч. 2-е изд., испр. – М.: 2013.
- Чеботаревская Т. М., Дрозд В. Л., Столяр А. А. Математика: учеб. для 4-го кл. общеобразоват. учреждений с рус. яз. обучения. В 2 ч. Ч. 2. – Минск: Нар. асвета, 2008.
Дополнительные ресурсы
- Интернет-портал «for6cl.uznateshe.ru»
- Интернет-портал «volna.org»
Домашнее задание
Попробуйте решить задачу № 3 другим способом:
- Расстояние между двумя велосипедистами составляет 240 м. Они выехали одновременно навстречу друг другу и встретились через 30 секунд. Какова скорость первого велосипедиста, если скорость второго равна 3 м/с?
- Из двух сел, расстояние между которыми составляет 30 км, одновременно вышли два пешехода. Один шел со скоростью 4 км/ч, а другой – со скоростью 5 км/ч. На сколько километров они сблизятся за 1 час пути? А за 3 часа?
Оцените урок:
До 2030 года: исчезнут 67 профессий и появятся новых 186 🤖
Посмотреть в Telegram



