Сложение отрицательных чисел
Мы продолжаем изучение сложения и вычитания положительных и отрицательных чисел. В этом уроке мы сосредоточимся на сложении отрицательных чисел. На основе ряда задач мы проиллюстрируем, что означает сложение отрицательных чисел, разберем алгоритм выполнения операций и выполним упражнения по этой теме.
Введение
Рассмотрим такой пример. На стоянку приехали 2 машины, а затем ещё 3 машины. Сколько свободных мест на стоянке, если всего мест 20 (рис. 1)?
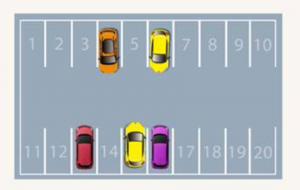
Рис. 1. Машины на стоянке
Изменится ли ответ на вопрос задачи, если на стоянку сначала приедут 3 машины, а затем 2? Или если приедут 4 машины, а затем ещё одна? Нет, потому что ![]() (рис. 2). Таким образом, с помощью сложения количества можно уменьшить количество запоминаемой (передаваемой) информации.
(рис. 2). Таким образом, с помощью сложения количества можно уменьшить количество запоминаемой (передаваемой) информации.
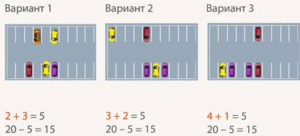
Рис. 2. Ответ на вопрос задачи не изменится
Но отрицательных количеств нет, зачем складывать отрицательные числа?
Пример. В кошельке 100 рублей. Потратили 5, 7, 13. Сколько осталось?
Решение
Способ 1. Мы можем вычитать последовательно: ![]()
Способ 2. Но можно рассуждать и по-другому. Уменьшить на 5, 7 и на 13, означает уменьшить на ![]()
Тогда мы от исходных 100 рублей сразу отнимаем ![]()
Ответ: осталось 75 рублей.
По сути во втором способе мы складывали отрицательные числа. Как мы это сделали? Мы сложили модули этих чисел и поставили перед суммой знак минус, показывая, что эту сумму нужно отнять.
Сумма двух отрицательных чисел
Сумму двух отрицательных чисел можно записать разными способами: ![]() . Чаще пишут без скобок (это короче): -4 — 12. Хотя теперь в записи нет знака плюс, это выражение эквивалентно исходному и является суммой двух отрицательных чисел. Складываем модули и ставим знак минус:
. Чаще пишут без скобок (это короче): -4 — 12. Хотя теперь в записи нет знака плюс, это выражение эквивалентно исходному и является суммой двух отрицательных чисел. Складываем модули и ставим знак минус:
![]()
Нам осталось сформулировать общее правило: чтобы сложить два отрицательных числа, нужно сложить их модули и поставить перед суммой знак минус. Результатом будет также отрицательное число:
![]()
Обобщение
Рассмотрим выражение -a -b. Воспользуемся тем, что мы уже знаем: ![]() , а также распределительным законом:
, а также распределительным законом:

Несложно убедиться, что эта общая формула согласуется с только что сформулированным правилом сложения отрицательных чисел.
Рассмотрим несколько примеров:
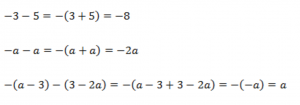
Примеры
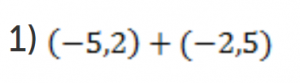
Запишем без скобок, чтобы было короче. Складываем модули слагаемых и ставим перед суммой
![]()
Складываем модули слагаемых и ставим перед суммой минус:
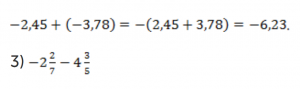
Складываем модули слагаемых и ставим перед суммой минус, отдельно складываем целые и дробные части:
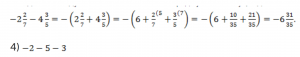
С тремя слагаемыми то же самое – складываем модули слагаемых и ставим перед суммой минус
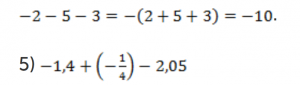
Второе слагаемое запишем в виде десятичной дроби. Сложение начнем с двух последних слагаемых, его можно проводить в любом порядке:
![]()
Уравнение
![]()
К обеим частям уравнения можно прибавить одно и то же число. Нам было бы удобно, чтобы в левой части уравнения остался только x без 2 (тогда в правой части получится значение переменной, то есть уравнение будет решено). Чтобы 2 пропало (превратилось в ноль), к нему нужно добавить противоположное число, то есть -2. Так и сделаем, добавим к обеим частям уравнения ![]()
2 и -2 дают в сумме ноль. Справа получили сумму двух отрицательных чисел. Делать это мы уже умеем.
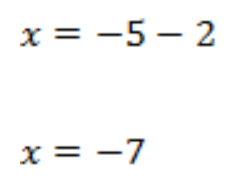
Повторение
Итак, повторим.
Складывать два отрицательных числа так же просто, как два положительных. Складываем числа, не обращая внимания на знак, потом ставим знак минус перед суммой: ![]()
Прибавление отрицательного числа равносильно вычитанию положительного. Поэтому сумму двух отрицательных чисел можно записать эквивалентными способами: ![]() .
.
Сложение отрицательных чисел с помощью числовой прямой
Проиллюстрируем сложение отрицательных чисел с помощью числовой прямой.
Мы уже знаем, чему равна сумма: ![]() .
.
Посмотрим, как это выглядит на числовой прямой. Первое слагаемое отмечаем точкой -4. Вычитание числа 3 (или прибавление числа -3) означает сдвиг влево на 3 единицы. Попадаем в точку -7 (рис. 3).
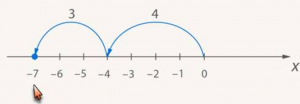
Рис. 3. Иллюстрация суммы
Поменяем слагаемые местами. От перемены мест слагаемых сумма не меняется: ![]() . На прямой это будет означать, что нам все равно, отступить от нуля влево сначала на 4 единицы, а потом на 3, или, наоборот, сначала на 3, а потом на 4. В любом случае получится точка, находящаяся слева от нуля на расстоянии 7, то есть с координатой -7 (рис. 4).
. На прямой это будет означать, что нам все равно, отступить от нуля влево сначала на 4 единицы, а потом на 3, или, наоборот, сначала на 3, а потом на 4. В любом случае получится точка, находящаяся слева от нуля на расстоянии 7, то есть с координатой -7 (рис. 4).
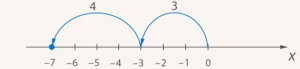
Рис. 4. Иллюстрация нахождения суммы
Заключение
Таким образом, в ходе этого урока мы освоили навыки сложения двух или более отрицательных чисел. На следующем занятии мы будем изучать сложение и вычитание всех известных нам чисел, включая как отрицательные, так и положительные.
Список рекомендованной литературы
- Зубарева И.И., Мордкович А.Г. «Математика. 6 класс». М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. «Математика. 6 класс. Учебник в 3 частях. Ч. 2». М.: «Просвещение», 2010.
- Виленкин Н.Я. и др. «Математика. Учебник для 6 класса». М.: ИОЦ «Мнемозина», 2013.
Дополнительные рекомендованные интернет-ресурсы
- Интернет-портал «math-prosto.ru»
- Интернет-портал «cleverstudents.ru»
Домашнее задание
- Выполните сложение:
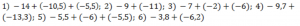
- Выполните сложение:
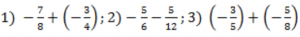
- Решите уравнение:
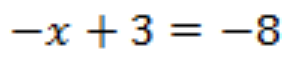
Оцените урок:
До 2030 года: исчезнут 67 профессий и появятся новых 186 🤖
Посмотреть в Telegram



