Конкретное значение действия «разделить»; разделить на равные части и разделить по содержанию

Давайте рассмотрим новую тему «Конкретное значение деления». Связь между умножением и делением».

Давайте решим первую задачу.

Положите по 2 кусочка сахара в каждую чашку. На сколько чашек хватит 8 кусочков сахара?

Давайте нарисуем 8 кусочков сахара. Весь этот сахар нужно разделить на 2 части, то есть по 2 в каждой чашке. Давайте покажем это действие на схеме дуги (рисунок 1).

Рисунок 2.1.1. 1. Иллюстративный пример

На рисунке показано, что 8 кусочков сахара хватает на 4 чашки, и ни одного кусочка сахара не остается. Говорят, что 8 частей были разделены на 2.

Давайте запишем решение задачи.

8:2 =4 (часа)

Ответ: На 4 чашки достаточно 8 кусочков сахара.

Давайте решим вторую задачу.

Равномерно распределите 8 кусочков сахара по 4 чашкам. Сколько кусочков сахара мне нужно положить в каждую чашку?

Рассуждаем таким образом. Поскольку в задаче указано «поровну», мне нужно разделить 8 кусочков на равные части. Следовательно, вам нужно найти количество предметов в каждой равной части. В каждую чашку положите по 1 кусочку сахара. Осталось всего 4 кусочка. Давайте добавлять по одному кусочку за раз. У меня закончились кубики сахара. Мы все разложили. В каждой чашке было по 2 кусочка сахара.

На рисунке это выглядит так (рис. 1). 2).

Рисунок 2.1.1. 2. Иллюстративный пример

Давайте запишем решение задачи.

Решение: 8:4=2 (К.)

Ответ: В каждую чашку нужно положить по 2 кусочка сахара.

Давайте сделаем выводы.

Теперь мы знаем 2 вида деления: деление на равные части и деление по содержанию.

Что значит разделить одно число a на другое число b?

Правильный ответ: Это означает, что нужно найти (подобрать) 3-е число c таким образом, чтобы при умножении его на число b получилось A.

Компоненты действия деления: «делитель», «Частное».

Теперь мы узнаем, как называются компоненты действия разделения (рис. 1). 3).

Рисунок 2.1.1. 3. Разделение компонентов

Выражение с символом деления между числами называется частным. Результат действия деления также называется частным.

У числа делений также есть название: число делений называется делимым.

Деление противоположно умножению

Как связаны действия деления и умножения?

Правильный ответ: Действие деления противоположно действию умножения.

Рассмотрим чертеж (рис. 1). 4).

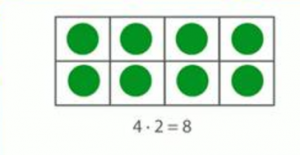
Рисунок 2.1.1. 4. Иллюстративный пример

Мы можем сказать так: это произведение чисел 4 и 2 означает, что в 1 ряду 4 круга, а таких рядов 2. Во 2 ряду 8 кругов.

Можно сформулировать это по-другому: на этой картинке 8 кружочков. Они были равномерно распределены в 2 ряда. Давайте выясним, сколько кружочков в 1 ряду. Для этого выполните действие разделения: 8:2. В каждом ряду по 4 кружочка.

Или можно сказать так: 8 кружочков были разделены на 4 равные группы, столбики. Давайте выясним, сколько кружочков в 1 столбике. Для этого нужно соотношение 8:4. В каждом столбике по 2 кружочка.

Обратите внимание, что число 8 в этой формуле является произведением, а 4 и 2 — множителями. Рассмотрим две другие формулы, относящиеся к произведению: 8 : 2 = 4, 8 : 4 = 2.

Давайте сделаем вывод: если вы разделите произведение 2 множителей на 1 из них, то получите еще один множитель.

Решите проблему и настройте противоположную задачу

Давайте решим задачу.

Высота каждого этажа дома составляет 3 м, а в доме 5 этажей. Какова высота дома от крыши (рис. 1). 5)?

Рисунок 2.1.1. 5. Иллюстративный пример

Мы рассуждаем таким образом. Высота каждого этажа равна 3 м, всего таких этажей 5. Следовательно, значение 3 м повторяется 5 раз. Ответить на поставленный вопрос можно, выполнив действие умножения.

Давайте запишем решение.

3*5=15(м)

Ответ: Высота дома составляет 15 метров до крыши.

Давайте составим эти 2 обратные задачи и решим их.

В обратной задаче мы знаем, что неизвестное становится известным, а известное — неизвестным.

Обратная задача № 1.

Высота 5-этажного здания составляет 15 метров. Какова высота каждого этажа дома (рис. 1). 6)?

Рис. 6. Иллюстрация к примеру

Рассуждаем так: высота дома – 15 м, таких этажей в доме – 5. Чтобы узнать высоту одного этажа, мы 15 делим на 5.

Запишем решение.

15 : 5 = 3 (м)

Ответ: высота каждого этажа дома – 3 метра.

Обратная задача № 2.

Высота каждого этажа дома – 3 м, а высота дома до крыши – 15 м. Сколько этажей в этом доме (рис. 7)?

Рисунок 2.1.1. 7. Иллюстративный пример

При решении задачи мы рассуждаем следующим образом: мы знаем, что высота дома до крыши составляет 15 м, а высота каждого этажа — 3 м.

Давайте запишем решение.

15:3=5(эт.)

Ответ: В этом доме 5 этажей.

На сегодняшнем уроке мы повторили конкретное значение действия «деление», узнали, как связаны между собой умножение и деление, как решать задачи и создавать обратные задачи для этого.

Список литературы

М.И.Моро, М.А.Бантова и другие. Математика: Учебное пособие. 3 класс: Часть 2, часть 1. -М.: «Просвещение», 2012.
М.И.Моро, М.А.Бантова и др. Математика: Учебное пособие. 3 класс: Часть 2, Ч. 2. -М.: «Просвещение», 2012.
М.И.Моро Уроки математики: методические рекомендации для учителей. 3 класс. -М.: Просвещение, 2012.
Нормативные документы. Мониторинг и оценка результатов обучения. -М.: «Просвещение», 2011.
«Русская школа»: программа для начальной школы. -М.: «Просвещение», 2011.
С.И.Волкова. Математика: Контрольные работы. 3 класс. -М.: Просвещение, 2012.
В.Н.Рудницкая. Тест. -М.: «Экзамен», 2012.

Дополнительные рекомендуемые ссылки на интернет-ресурсы

Интернет-портал»nsportal.ru «(Источник)

Домашнее задание

1. Используйте рисунок для решения задачи.

В саду было посажено 4 ряда яблонь, и в каждом ряду было посажено по 3 яблони. Сколько яблонь было посажено в саду?

В саду было посажено 12 яблонь, по 3 в каждом ряду. Во сколько рядов посажены яблони?

В саду было посажено 4 ряда по 12 яблонь. Сколько яблонь было посажено в каждом ряду?

2. Используйте рисунок для решения задачи. Настройте обратные задачи на это и решите их.

На парковке было 4 ряда автомобилей, и в каждом ряду было по 6 машин. Сколько машин было на парковке?

3. Подумайте сами о задачах, которые решаются путем умножения. Настройте обратные проблемы таким образом и решите их.