Сложение и вычитание смешанных чисел
В этом уроке вы узнаете, что такое смешанные числа, как обычно записываются смешанные числа, как складывать и вычитать смешанные числа (как положительные, так и отрицательные) и как вычитать соответствующие дроби из целых чисел.
Введение
Тема урока: «Сложение и вычитание смешанных чисел».
Но дело в том, что это не новые числа. Смешанное число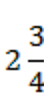 
– это два и еще 3/4. Просто сумма двух чисел.
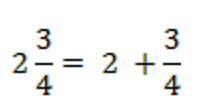
Мы уже знаем, как складывать целые и дробные числа. То же самое касается и сложения смешанных чисел: сложения целых чисел и сложения обыкновенных дробей. Нам нужно использовать те знания, которые у нас уже есть. Все, что нам нужно, — это подумать, почему мы пишем и называем их так, как пишем, и использовать примеры, чтобы убедиться, что нам не нужно изучать никаких новых знаний или правил.
Пример 1
Отложить два смешанных числа: 
Напишем у каждого знак «+».
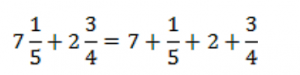
Теперь мы лучше видим все 4 слагаемых. Сложим теперь так, как нам удобнее.
Целые числа 7 и 2 сложить легко.
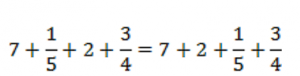
Обыкновенные дроби мы тоже умеем складывать. Приведем их к общему знаменателю.
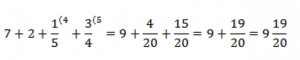
Ответ: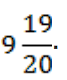 
.
Пример 2
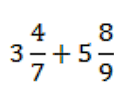
Поставим знаки «+»:
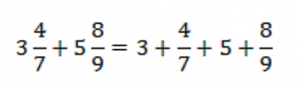
Сложим отдельно целые числа и отдельно обыкновенные дроби.
Дробь 
уже можно записать как смешанную, убрав знак плюс, но обыкновенную дробь можно записать и проще. Выделим целую часть.
К целой части добавляется еще единица.
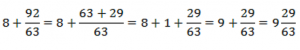
Ответ: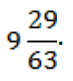 
.
Пример 3
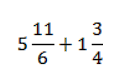
Поставим знаки «+»:
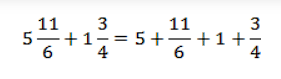
Можно сложить отдельно целые числа и дроби, но у дроби 11/6 можно выделить целую часть, станет проще.
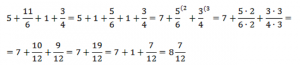
Ответ: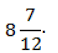 
Вычитание смешанных дробей
Как вычитать? Это тоже просто. Как написать минус перед смешанной дробью? Минус относится к целой дроби. Вы можете поставить скобку и минус перед ней, а можете раскрыть скобку. Каждая сумма будет иметь минус.
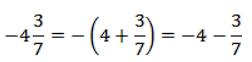
Пример 4
Пример 5
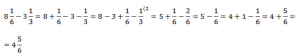
Полезным навыком здесь является умение вычитать правильную дробь из единицы или другого целого числа.
Вычитание правильной дроби из целого числа
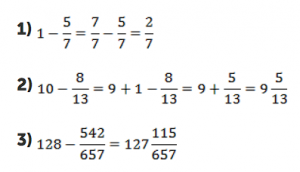
Сложение двух отрицательных смешанных дробей не представляет проблемы.
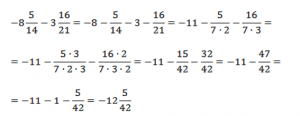
Не обязательно все подробно записывать. Если вы уверены в себе, то сможете многое сделать в голове.
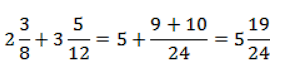
Задание
Самостоятельно выполните несколько заданий, а потом проверьте.
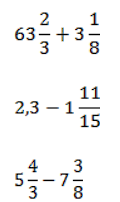
Смешанные числа
Дроби нужны для записи величин, которые не являются целыми числами: треть пути, четверть часа, половина яблока. Это все примеры величин, меньших единицы: 1,5 литра молока, 2,5 часа, 3,5 километра. Как удобнее всего записать эти величины? Если семь яблок нужно разделить между тремя людьми, есть два способа:
1) Каждое яблоко делим на три части и раздаем эти части всем участникам. Каждый такой кусочек – это 1/3 яблока.
В итоге каждый получит 7 таких кусочков: 7/3.
2) Проще каждому раздать по два яблока. А оставшиеся разделить на три части и раздать. Все-таки легче резать одно яблоко, чем семь.
В итоге каждый получит по два целых и еще по одной трети: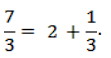 
.
Это разные записи одного и того же количества.
Такие количества, целое плюс дробное, встречаются часто.
Чтобы упростить запись, договорились, что можно не писать знак «+»:
.
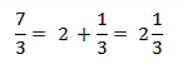
В последней записи смешались целое и дробное число. Поэтому такую запись назвали смешанным числом или смешанной дробью.
И неправильная дробь, и смешанная обозначают одно и то же количество.
Какая удобнее? Это зависит от ситуации.
По смешанной легче представить количество.
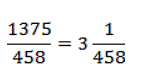
По левой записи мы понимаем только, что это число больше единицы. А вот по правой – что число почти равно трем, чуть-чуть больше трех, на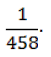 
Удобнее складывать и вычитать дроби как смешанные числа, а умножать и делить как обычные дроби. Десятичные дроби очень близки к смешанным числам и практически идентичны им. Обозначения разные, но смысл один и тот же. Сначала запишите целое число, затем дробную часть.
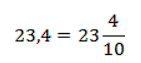
Если у десятичной дроби целая часть равна нулю, то она легко записывается обыкновенной правильной дробью, просто ноль целых в смешанной дроби не пишем.
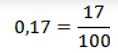
Итак, между целой и дробной частями смешанной дроби пропущен знак «+». Если это помнить, то не нужно никаких дополнительных правил.
Чтобы превратить смешанную дробь в обыкновенную, нужно сложить целое число и дробь.
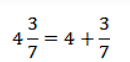
Чтобы сложить целое число с дробью, представим 4 как дробь со знаменателем единица, приведем ее к знаменателю 7, домножив числитель и знаменатель на 7.
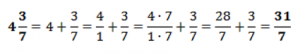
Или, в другую сторону, вынесем целую часть из неправильной дроби.
Нам давно знаком этот способ. Деление столбиком с остатком – это и есть вынесение целой части.
Вернемся к 7 яблокам, которые мы делим на троих.
Разделим столбиком 7 на 3 с остатком.
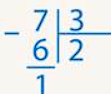
Ответ: 2 и 1 в остатке. То есть по два целых яблока уже досталось всем, и одно осталось. Его нужно делить на три части.
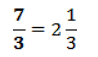
Конечно, в таком простом случаем мы обойдемся без деления столбиком.
Число 7 больше трех и не делится на три. Его можно разбить на две части – часть, которая делится на 3 – 6, и остаток, который меньше трех, – 1. 6 яблок делится на 3, это два, и еще одно делим на три. Это 1/3.
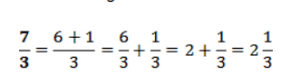
В более сложных случаях все-таки нужно воспользоваться делением в столбик.
221/8
Чтобы вынести целую часть, разделим числитель на знаменатель в столбик.
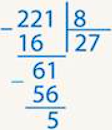
Получили 27 и 5 в остатке. То есть, мы разбили число 221 на две части: первая, которая делится на 8 и дает в результате 27 (саму эту часть мы не видели, но нетрудно догадаться по остатку, что она равна 216) и остаток, меньший 8, – это 5:
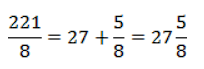
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика для 6 класса. – Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математики для 5–6 классов. – ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика для 5-6 классов. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.
Дополнительные рекомендованные онлайн-ресурсы
- Интернет-портал «school-assistant.ru» (Источник)
- Интернет-портал «urok.1sept.ru» (Источник)
Домашнее задание
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012. № 376.
2. 
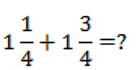
3. 
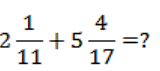
Оцените урок:
