Введение

Мы знаем, что с помощью знака равенства разными способами записываются эквивалентные выражения.

Например, (действительно, если на складе лежало 5 мячей и 5 мячей оттуда забрали, то на складе ничего не осталось).

С другой стороны, (действительно, мы определяли противоположное число -a так, что Как видим то есть вычитание равносильно сложению с противоположным числом: .

Но тогда для вычитания мы можем пользоваться уже известными нам правилами сложения с одинаковыми или разными знаками.

Вычитание

Рассмотрим примеры.

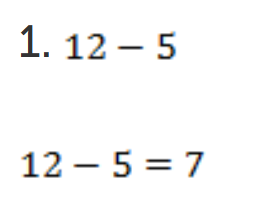
Но эту же разность, 12 — 5, еще можно считать суммой двух чисел  . Так как знаки разные, надо от большего модуля отнять меньший и поставить знак числа с большим модулем, в данном случае – плюс.

Эту разность можно считать суммой двух отрицательных чисел: . Так как знаки одинаковые, то складываем модули и ставим знак минус: .

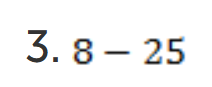
Это сумма положительного числа 8 и отрицательного. От большего модуля отнимаем меньший и ставим знак числа с большим модулем, то есть минус: .

Получается, нам не нужны новые правила, чтобы вычитать из одного числа другое. Достаточно знать правила сложения чисел с разными знаками.

Примеры

Оба слагаемых одного знака. Складываем модули, ставим знак минус:

.

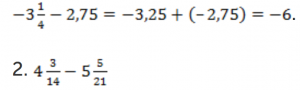Слагаемые разных знаков. Нужно от большего модуля отнять меньший и поставить впереди знак числа с большим модулем. То есть знак минус: 

Вычитание числа -26 можно заменить прибавлением противоположного числа 26. Или, если короче, два минуса перед числом дают плюс: .

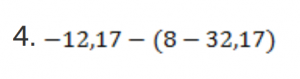
Выполняем действие в скобках, результат будет отрицательным. Два минуса перед числом дают плюс. Слагаемые имеют разные знаки, значит, вычитаем из большего модуля меньший, ставим знак плюс в ответе: 

Этот же пример можно было выполнить по-другому. Знак минус перед скобкой относится к каждому слагаемому в скобках, то есть меняет его знак. Раскрываем скобки, меняя знак каждого слагаемого. Первое и последнее слагаемые легко складываются. Они разных знаков, вычитаем из большего модуля меньший. Ответ тот же самый: 

Расстояние между точками на координатной прямой

Рассмотрим такой пример. Найдём расстояние между точками, соответствующими числам 3 и 8 на координатной прямой. Несложно увидеть, что оно равно

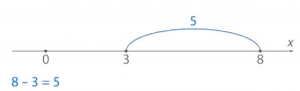
Рис. 1. Расстояние между данными точками

То есть чтобы найти расстояние между точками на числовой прямой, совсем не обязательно строить координатную прямую, отмечать точки. Нужно просто из большего числа вычесть меньшее.

Убедимся, что это правило верно независимо от того, какой знак у чисел, соответствующих этим точкам. Найдем расстояние между точками, координаты которых – числа с разными знаками, например, между -4 и 7. Расстояние от -4 до 7 равно сумме расстояний от этих чисел до нуля. Но получается, для вычисления расстояния мы используем третье число 4, которого не было в условии (рис. 2).

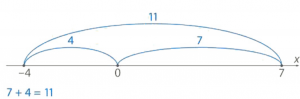
Рис. 2. Расстояние  между точками -4 и 7

Это не очень удобно. Давайте попробуем обойтись только теми числами, которые есть в условии задачи. Пользуясь тем, что прибавление числа эквивалентно вычитанию противоположного (или, коротко, два минуса подряд дают плюс), мы можем переписать нашу сумму:

Здесь уже участвуют только те два числа, что были в условии. Но это снова разность двух чисел: из большего мы вычитаем меньшее. То есть чтобы найти расстояние между двумя числами с разными знаками, нужно из большего (положительного) вычесть меньшее (отрицательное).

Нам осталось рассмотреть последний случай: расстояние между точками, координаты которых – отрицательные числа. Найдем расстояние между -9 и -6 Расстояние от нуля до -9 равно 9, до -6 равно 6. Чтобы найти расстояние между точками, нужно из 9 вычесть 6: 9 — 3 = 6. Мы снова использовали числа, которых не было в условии (рис. 3).

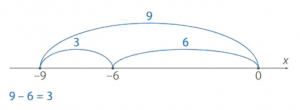
Рис. 3. Расстояние между числами -9 и -6

Сделаем эквивалентную замену: .

У нас получилась разность двух исходных чисел. Причем первое число (-6) больше второго (-9). То есть чтобы найти расстояние между отрицательными числами, нужно из большего вычесть меньшее.

То есть во всех трех случаях получилось одно и то же правило. Давайте его еще раз повторим: чтобы найти расстояние между двумя точками на числовой прямой, нужно из большей координаты вычесть меньшую: .

Если мы не знаем, какое число больше, а какое меньше то мы не можем записать просто a — b или b — a, ведь так мы можем получить отрицательное значение расстояния.

Чем отличаются эти два выражения? Только знаком. Например, . Действительно: То есть эти разности ­– противоположные числа, а значит, их модули равны. Таким образом, мы можем сказать коротко: расстояние между точками на координатной прямой равно модулю разности их координат: .

Давайте потренируемся. Без построения числовой прямой найти расстояние между двумя числами.

Из большего числа вычитаем меньшее. Из двух отрицательных чисел больше то число, модуль которого меньше:

Из большего числа вычитаем меньшее. Положительное число всегда больше отрицательного:

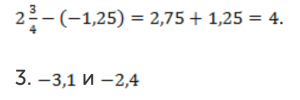
Из большего числа вычитаем меньшее. Из двух отрицательных чисел больше то число, модуль которого меньше:

Нахождение расстояния между двумя точками заставляет задуматься еще об одном факте. Если из большего числа вычесть меньшее, всегда получим положительное число (расстояние), даже если одно или оба числа были отрицательными.