Составные задачи на нахождение уменьшаемого, вычитаемого и разности
Давайте повторим определение составных задач.
Составные задачи – это задачи, для решения которых необходимо выполнить несколько шагов, чтобы получить ответ на главный вопрос.
Теперь вспомним, какие элементы входят в действие вычитания. Уменьшаемое и вычитаемое – это два ключевых компонента вычитания. Какой результат мы получаем в результате этого действия? Ответом является разность, которая также является результатом вычитания.
Решение задачи 1
Задача 1

Рис. 1. Задача 1
Решение.
Решение задачи 1
Задача 1
Условие.
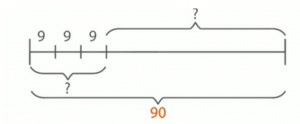
На рис. 2 представлена схема задачи, в которой известно общее количество роз – 90. Это число является уменьшаемым, состоящим из двух частей: вычитаемого и разности. В данной задаче вычитаемое нам неизвестно, но мы можем его определить, узнав, сколько роз в трех букетах. Неизвестное значение в этой задаче – это разность, которую мы найдем во втором действии.
Первым шагом нам необходимо выяснить, сколько роз находится в трех букетах. Поскольку букеты одинаковые и в каждом из них по 9 роз, чтобы узнать общее количество роз в трех букетах, нужно умножить 9 на 3:
- 9×3=279×3=27 (р.)
Теперь мы можем найти, сколько роз осталось. Для этого нам нужно определить разность. Чтобы найти разность, необходимо вычесть вычитаемое из уменьшаемого. Из общего количества роз, которое привезли в магазин (90), вычтем количество роз в букетах (27):
- 90−27=6390−27=63 (р.)
Ответ: 63 розы.
В этой задаче мы находили разность, и такие задачи называются задачами на нахождение разности.
Решение задачи 2
Задача 2

Рис. 3. Задача 2
Решение.
Решение задачи 2
Задача 2
Условие.
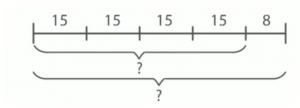
На рис. 4 представлена схема задачи, где известны некоторые части. Мы пока не знаем, сколько учебников на полках, но можем это вычислить. Известно, что 8 учебников еще не были поставлены на полки. Неизвестное в этой задаче – целое, которое в данном случае является уменьшаемым. Таким образом, мы решаем задачу на нахождение уменьшаемого.
Чтобы найти уменьшаемое, нам нужно знать вычитаемое и разность. Правило для нахождения уменьшаемого гласит, что мы должны прибавить вычитаемое к разности. Однако вычитаемое нам пока неизвестно, и мы начнем с его вычисления.
Если на каждой полке стоит 15 учебников, а полок всего 4, то мы можем узнать, сколько учебников находится на всех полках. Для этого умножим количество учебников на одной полке (15) на количество полок (4):
- 15×4=6015×4=60 (кн.)
Теперь у нас есть 60 учебников на полках, и 8 учебников еще не поставлены. Чтобы узнать общее количество учебников, которые привезли в библиотеку, нам нужно сложить количество учебников на полках (60) и количество оставшихся учебников (8):
- 60+8=6860+8=68 (кн.)
Ответ: Всего в библиотеку было привезено 68 книг.
Решение задачи 3
Задача 3
Условие.
Теперь давайте определим, что именно неизвестно в задаче 3. В этой задаче мы будем работать с новыми данными и постараемся выяснить, какие значения нам нужно найти и каким образом мы можем это сделать.
(Здесь можно продолжить с конкретным условием задачи 3, если оно имеется.)

Рис. 5. Задача 3
Решение.
Давайте выясним, что неизвестно в данной задаче.
Решение задачи 3
Задача 3
Условие.
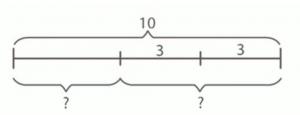
На схеме, представленной на рис. 6, видно, что у Винни Пуха было 10 бочонков с медом. Это число является целым, то есть уменьшаемым, и оно нам известно. Однако количество бочонков, которые Винни Пух отдал Кролику, пока неизвестно, и это является основным вопросом задачи. Мы также знаем, что оставшиеся бочонки Винни Пух разместил на двух полках, по 3 бочонка на каждой. Нам нужно выяснить, сколько бочонков находится на полках.
В этой задаче нам необходимо найти вычитаемое. Для этого мы будем вычитать разность из известного уменьшаемого. Начнем с нахождения разности.
У Винни Пуха на двух полках по 3 бочонка. Чтобы узнать, сколько всего бочонков стоит на полках, нужно умножить количество бочонков на одной полке (3) на количество полок (2):
- 3×2=63×2=6 (б.)
Таким образом, из 10 бочонков, 6 находятся на полках, а остальные Винни Пух отдал Кролику. Чтобы узнать, сколько бочонков с медом Винни Пух подарил своему другу, воспользуемся формулой: из уменьшаемого вычтем разность, и получим вычитаемое:
- 10−6=410−6=4 (б.)
Ответ: Винни Пух подарил Кролику 4 бочонка.
Выводы
На сегодняшнем уроке мы познакомились с новым типом задач и научились правильно рассуждать для их решения. На следующем уроке мы будем решать составные задачи, связанные с разностным и кратным сравнением.
Список литературы
- Александрова Э. И. Математика. 2 класс. – М.: Дрофа, 2004.
- Башмаков М. И., Нефёдова М. Г. Математика. 2 класс. – М.: Астрель, 2006.
- Дорофеев Г. В., Миракова Т. И. Математика. 2 класс. – М.: Просвещение, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «mat-zadachi.ru» (Источник)
Домашнее задание
(Здесь можно указать конкретные задания для выполнения дома.)
1. Какие задачи называются составными? Компонентами какого действия является уменьшаемое и вычитаемое?
2. Решите задачу.
Ежик собрал 28 яблок. 9 из них он отдал ежику и еще несколько белочке. Сколько ежик отдал яблок белочке, если у него осталось 12 яблок?
3. Решите задачу.
В банке были соленые огурцы. За завтраком съели 12 огурцов, а в обед – 21. Сколько огурцов было в банке, если в ней осталось 15 огурцов?
4. * Решите задачу.
Туристы прошли в первый день 5 км, во второй день – 3 км. Сколько всего км им надо пройти, если осталось пройти 2 км?
Оцените урок:




