Умножение обыкновенных дробей
В этом уроке вы узнаете правила умножения дробей. Вы научитесь умножать дроби и натуральные числа, умножать дроби и умножать смешанные числа. Каждое правило сопровождается поясняющим вопросом. В процессе решения задачи уточняется постановка вопроса.
Правила умножения обыкновенных дробей
Вывод правил умножения обыкновенных дробей Существует формула, которая позволяет перемножить две обыкновенные дроби. В этом уроке мы попытаемся вывести правила умножения обыкновенных дробей.
Для этого рассмотрим такую задачу: найти площадь прямоугольника, одна из сторон которого – 2/3 дм, а другая – 4/5 дм.
Вспомним, что площадь прямоугольника – это произведение его сторон. Чтобы найти площадь, нужно умножить 2/3 на 4/5, но именно этого мы пока не умеем. Давайте решим эту задачу другим способом.
Нарисуем прямоугольник размером 1 дм на 1 дм, который является квадратом, так как его длина равна ширине. Далее разделим одну из его сторон на 5 равных частей, а другую сторону – на 3 равные части (см. рис 1). Мы получили 15 равных прямоугольников.
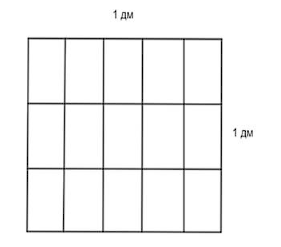
Вспомним, что по условию задачи нам нужно найти площадь прямоугольника, одна из сторон которого – 2/3 дм, а другая – 4/5 дм. То есть найти площадь закрашенного зелёным цветом прямоугольника (рис. 2).
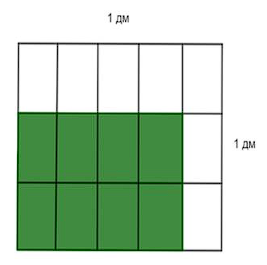
Рис. 2. Прямоугольник зелёного цвета со сторонами 2/3 дм и 4/5 дм
Как её найти? Площадь всего прямоугольника – 1 дм в квадрате, он разделён на 15 равных прямоугольников, а закрашено 8. Тогда площадь закрашенной части – 8/15 дм в квадрате.
Мы нашли площадь, не перемножая обыкновенные дроби, но мы знаем, что эту же площадь можно представить как произведение двух обыкновенных дробей:
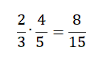
Теперь из этого примера попытаемся вывести правило умножения обыкновенных дробей.
Вспомним, что мы делали:
- Разбили квадрат на 15 равных частей. Знаменатель одной дроби равен 5, другой – 3. Стороны квадрата разбили на соответственно равные части, и 5 * 3 = 15. То есть 15 – это произведение знаменателей исходных дробей.
- Как появилась 8? Мы брали 2/3, то есть 2 части из 3 (как одна сторона), и 4/5,то есть 4 части из 5. И 2 * 4 = 8.
Таким образом,
чтобы перемножить две дроби, необходимо перемножить их числители и записать результат в числитель, затем перемножить знаменатели и записать полученный результат в знаменатель. |
Решение примеров
Пример 1.
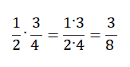
Пример 2.
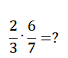
Обратите внимание, что 3 и 6 можно сократить, и лучше выполнять сокращение сразу при умножении, а не при записи ответа.
Таким образом, 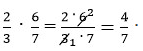 .
.
Сокращать дроби можно только в том случае, если в числителе и в знаменателе записано произведение.
Пример 3.
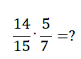
Если не сократить дроби на данном этапе, то необходимо будет сокращать дробь 70/105. Поэтому облегчим задачу и сократим дробь при умножении.
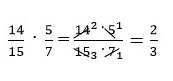
Рассмотрим пример умножения дроби на смешанное число.
Пример 4.
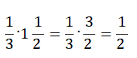
Можно сформулировать правило:
если в произведении множитель является смешанным числом, его необходимо перевести в неправильную дробь, а затем выполнить умножение |
Теперь рассмотрим пример, когда оба сомножителя являются смешанными числами.
Пример 5.
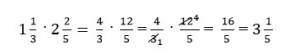
Как умножить дробь на целое число? Вспомним, что целое число можно представить в виде неправильной дроби: 3 можно представить как 3/1, число 2 как 2/1 и так далее. Давайте рассмотрим пример.
Пример 6.
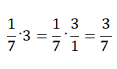
Пример 7.
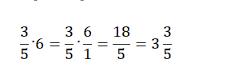
Решение задачи. Умножение нескольких обыкновенных дробей
Решение задачи
Решим следующую задачу: предположим, велосипедист едет со скоростью ![]() км/ч в течение
км/ч в течение ![]() часа. Какой путь проехал велосипедист?
часа. Какой путь проехал велосипедист?
Запишем условие задачи.
Дано:
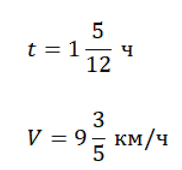
Найти:
S – ?
Решение:
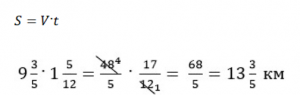
Ответ: ![]() .
.
Важно, что при решении задачи мы сократили дроби прежде, чем их перемножили.
Давайте посмотрим на пример, который иллюстрирует, что было бы, если бы мы перемножали дроби без сокращения.
Пример 8.
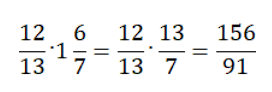
Получившуюся дробь можно сократить только на 13. Догадаться, что у 156 и 91 есть общий делитель 13, не так-то просто. Конечно, некоторые это сделать могут, но проще было сократить дробь при умножении и получить ответ 12/7 или ![]() .
.
Пример умножения нескольких обыкновенных дробей
Теперь рассмотрим примеры, когда перемножаются не две дроби, а больше.
Пример 9.
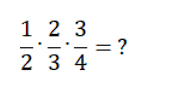
Например, такие вычисления могут возникнуть при нахождении объёма параллелепипеда со сторонами ![]() м. Умножение в данном случае выполняется точно так же, как в случае с двумя дробями. Умножаем числители – записываем в числитель, умножаем знаменатели – записываем в знаменатель.
м. Умножение в данном случае выполняется точно так же, как в случае с двумя дробями. Умножаем числители – записываем в числитель, умножаем знаменатели – записываем в знаменатель.

Пример 10.
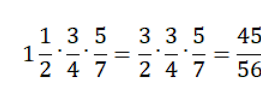 . Дробь несократима, так как иначе мы бы сократили её на этапе умножения.
. Дробь несократима, так как иначе мы бы сократили её на этапе умножения.
Заключение
Таким образом, в ходе нашего занятия мы освоили умножение обыкновенных дробей. Мы выяснили, что этот метод также подходит для перемножения смешанных и целых чисел, а также убедились, что он работает и для трех и более дробей.
Список рекомендуемой литературы
- Математика 6. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. М. – Мнемозина, 2012.
- Математика для 6 класса. Мерзляк А. Г., Полонский В. В., Якир М. С. – Гимназия, 2006.
- За страницами учебника математики. Депман И. Я., Виленкин Н. Я. – Просвещение, 1989.
- Задания по курсу математики для 5-6 классов. Рурукин А. Н., Чайковский И. В. – ЗШ МИФИ, 2011.
- Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. Рурукин А. Н., Сочилов С. В., Чайковский К. Г. – ЗШ МИФИ, 2011.
- Математика: Учебник-собеседник для 5-6 классов средней школы. Шеврин Л. Н., Гейн А. Г., Коряков И. О., Волков М. В. – Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные онлайн-ресурсы
- Интернет-портал «matematika-na.ru» (Источник)
Домашнее задание
Для выполнения домашнего задания используйте Математика 6 под редакцией Виленкина Н. Я., Жохова В. И., Чеснокова А. С., Шварцбурда С. И. М. (ссылка см. 1.2).
Задания: № 472 (а, б, ж, з, к, м), № 474, № 476.
Дополнительные задания: № 478 (а, в), № 433.
Оцените урок:




