Изменение площадей и объёмов
На данном уроке вы познакомитесь с тем, как площадь и объем геометрических фигур изменяются при увеличении или уменьшении их сторон. Мы решим несколько задач и рассмотрим примеры, которые помогут вам лучше усвоить материал. На основе ваших наблюдений вы сможете вывести правила, которые упростят решение аналогичных задач в будущем.
Если у вас возникнут трудности с пониманием темы, рекомендуем ознакомиться с уроками «Измерение» и «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур».
Задача № 1: Изменение площади
Для начала давайте рассмотрим одну задачу и решим её двумя способами: математически и графически.
Задача 1
Если каждую сторону прямоугольника увеличить в два раза, во сколько раз изменится его площадь (см. рис. 1)?
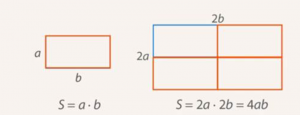
Ответ: площадь увеличится в четыре раза.
Формулировка правила
Таким образом, если увеличить стороны фигуры в три раза, то площадь возрастет в девять раз, а если в четыре раза — в шестнадцать раз. Правильна ли эта закономерность для других фигур? Давайте это проверим.
На основе проведенных наблюдений можно сделать вывод, что если все стороны фигуры увеличить в kk раз, то площадь увеличится в k2k2 раз (или k×kk×k) (см. рис. 2).
Ситуация аналогична и в случае уменьшения сторон фигуры. Например, если стороны фигуры уменьшить в два раза, то площадь, соответственно, сократится в четыре раза.
Пример № 1: Применение сформулированного правила
Для замощения улицы А потребовалось 1000 кирпичей (см. рис. 3). Улица В по всем измерениям больше улицы А в два раза. Сколько кирпичей понадобится для замощения улицы В?
Решение:
1000 * 4 = 4000
Ответ: 4000 кирпичей
Пример № 2 на применение сформулированного правила
В семье живут отец и сын. Отец крупнее сына в два раза по всем измерениям (по высоте, ширине и т. д.). Если сыну на рубашку требуется 1,5 m² ткани, то сколько ткани потребуется отцу? (см.рис.№4)

Рис. 4. Иллюстрация к примеру № 2
Решение:
1,5 * 4 = 6
Ответ: 6 m² ткани.
Пример № 1 изменения объема и формулировка правила
Теперь возникает вопрос: а как насчет объемных тел, что происходит при увеличении или уменьшении всех их сторон? Давайте возьмем куб и увеличим все его измерения в два раза. Тогда его объем изменится в 8 раз, как на рисунке 5.
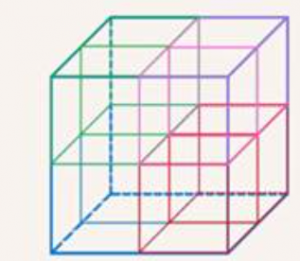
Рис. 5. Увеличение куба
Тогда мы можем утверждать: если все измерения фигуры увеличились в ![]() раз, то объем фигуры увеличится в
раз, то объем фигуры увеличится в ![]() раз
раз
Задача № 1 на изменение объема
Одного куска мыла семье хватает на месяц. На сколько времени им хватит куска мыла, которое будет вдвое больше по всем измерениям, чем исходный кусок (рис. 6)?

Рис. 6. Иллюстрация к задаче № 1
Решение:
1 * 8 = 8
Ответ: 8 месяцев.
Скоро вы узнаете из уроков физики, что при одинаковой плотности вещества его масса пропорциональна его объему (если объем увеличится в x раз, то и масса увеличится в x раз). Давайте решим еще одну задачу.
Задача № 2 на изменение объема
В зоопарке есть два слона, один из которых превосходит другого по всем измерениям ровно в 2 раза. Для того чтобы прокормить первого, необходим 1 кг корма. Сколько килограммов корма нужно для второго слона (рис. 6)?

Рис. 7. Иллюстрация к задаче № 2
Решение:
8 * 1 = 8
Ответ: 8 кг.
Повторение пройденного на уроке
Мы изучили, как изменяются площадь и объем фигуры при увеличении или уменьшении ее сторон.
Повторение изученного на уроке
На занятии мы рассмотрели, как изменяются площадь и объем фигур при увеличении или уменьшении их сторон.
Список литературы
- Виленкин Н.Я. Математика. 6 класс. Учебник. – 2014.
- Никольский С.М., Потапов М.К. Математика. 6 класс. Учебник. – М.: 2012. – 256 с.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 6 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Домашнее задание
- Если все стороны прямоугольника увеличиваются в пять раз, во сколько раз изменится его площадь?
- Если размеры куба увеличиваются в три раза, во сколько раз возрастет его объем?
Дополнительные рекомендованные интернет-ресурсы
- Интернет-портал «mccme.ru» (Источник).
- Интернет-портал «kokch.kts.ru» (Источник).
Оцените урок:




