Главная > Единица площади — квадратный метр
Единица площади - квадратный метр
Знайте единицу измерения площади – квадратные метры
Известно, что площадь фигуры можно измерить в квадратных сантиметрах. Как вы думаете, как можно назвать единицу площади, равную площади квадрата со стороной 1м? Все верно — это квадратный метр. Слово «квадратный метр» в цифрах пишется следующим образом: 8 м2, 20 м2. Эта единица измерения используется, например, при измерении площади комнаты, дома или сада. Комнаты, квартиры, дома, земельные участки, большие площади города рисуются на бумаге в уменьшенном виде.
Найдите площадь фигуры
Например, на этом рисунке показан план загородного дома, в котором 1 ячейка условно принимается за площадь в 1 м2 (рисунок 1). 1).
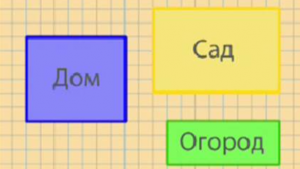
Рисунок 2.1.1. 1. Планировка
Площадь дома на плане равна 42 ячейкам, что означает, что его фактическая площадь составляет 42 м2.
Площадь сада и площадь огорода мы узнаем в соответствии с планом.
Видно, что длина сада на плане равна 9 ячейкам, то есть 9 м, а ширина — 6 ячейкам, то есть 6 м. Следовательно, чтобы найти площадь прямоугольника, нужно умножить длину на ширину.
Давайте запишем решение.
9*6=54(м2)
Ответ: Площадь сада равна 54 м2.
Длина сада равна 8 ячейкам, то есть 8 м, а ширина равна 3 ячейкам, то есть 3 м. Для этого умножьте длину на ширину.
Запишем решение.
8*3=24(м2)
Ответ: Площадь сада равна 24 м2.
Установите соответствие между М2 и дм2.
Как вы думаете, на сколько квадратов со сторонами 1 м можно разбить квадрат со сторонами 1 м (рис. 1). 2)?
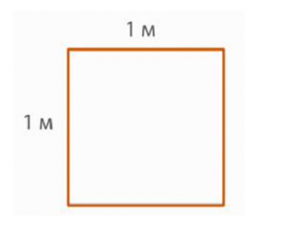
Рис. 2. Квадратный метр
Установим соотношение между квадратным дециметром и квадратным метром. Будем рассуждать так. Поскольку квадрат со стороной 1 м можно разбить на 10 полосок, в каждой из которых по 10 дм2, то всего в квадратном метре десять десятков, или сто квадратных дециметров (рис. 3).
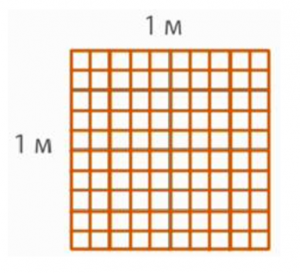
Рисунок 2.1.1. 3. Сто квадратных дециметров
Давайте запомним
1м2=100дм2
Выполнение задания по переводу единиц измерения площади
Давайте потренируемся. Давайте выразим это в квадратных дециметрах.
5 м2 = … дм2
8 м2 = … дм2
3 м2 = … дм2
Рассуждаем так. Мы знаем, что в квадратном метре сто квадратных дециметров. Значит, в пяти квадратных метрах – пятьсот квадратных дециметров.
Проверьте себя.
5 м2 = 500 дм2
8 м2 = 800 дм2
3 м2 = 300 дм2
Разгадайте правило, по которому записан каждый ряд величин, и продолжите его.
93 см, 8 дм 6 см, 79 см, …
1 дм2, 90 см2, 80 см2, …
96 дм2, 1 м2, 104 дм2, 1 м2 8 дм2, …
Рассмотрим первую строку.
93 см, 8 дм 6 см, 79 см, …
Мы видим три линейные величины. Вспомним о том, что 1 дм = 10 см. Чтобы удобнее было сравнивать, переведём все величины в одни единицы измерения, в сантиметры. Переводим: 8 дм 6 см = 86 см. Величины стоят в порядке убывания. Каждая следующая величина уменьшается на 7 см. Значит, 79 см уменьшаем на 7 см, получаем 72 см и эту величину выразим в дм и см: 72 см = 7 дм и 2 см.
93 см, 8 дм 6 см, 79 см, 7 дм 2 см
Рассмотрим вторую строку.
1 дм2, 90 см2, 80 см2, …
Можем сказать, что во второй строке записаны единицы площади. Переведём 1 дм2 в квадратные сантиметры. Помним, что 1 дм2 = 100 см2. Получился ряд величин 100 см2, 90 см2, 80 см2, … Можем сделать вывод о том, что каждая следующая величина уменьшается на 10 см2. Значит, следующая величина в этом ряду должна быть 70 см2.
1 дм2, 90 см2, 80 см2, 70 см2
Рассмотрим третью строку.
96 дм2, 1 м2, 104 дм2, 1м2 8 дм2, …
В третьем ряду тоже записаны единицы площади. Выразим все величины в квадратных дециметрах. Помним, что 1 м2 = 100 дм2. Это значит, что 1 м2 8 дм2 = 108 дм2. Получили ряд величин: 96 дм2, 100 дм2, 104 дм2, 108 дм2, видим, что величины расположены в порядке возрастания. Каждая следующая величина больше предыдущей на 4 дм2. Следовательно, продолжит этот ряд величина 112 дм2.
96 дм2, 1 м2, 104 дм2, 1 м2 8 дм2, 112 дм2
Выполните тренировочные упражнения по теме урока
Давайте выполним следующие задания.
Умножьте каждое значение на 1 м2
10 дм2 + … дм2 = 1 м2
24 дм2 + … дм2 = 1 м2
62 дм2 + … дм2 = 1 м2
Необходимо вспомнить, что 1 м2 = 100 дм2
Тогда рассуждать будем так: сумма двух величин должна равняться 1 м2 или 100 дм2. Поэтому к первому слагаемому надо прибавить столько, чтобы получилось 100 дм2 или 1 м2.
Проверьте себя.
10 дм2 + 90 дм2 = 1 м2
24 дм2 + 76 дм2 = 1 м2
62 дм2 + 38 дм2 = 1 м2
Решите задачу двумя способами.
Площадь трёх комнат равна 44 м2. Площадь первой комнаты составляет 24 м2, площадь второй комнаты – 8 м2. Чему равна площадь третьей комнаты?
Способ 1.
Сначала от общей площади комнат вычтем площадь первой комнаты, а затем от полученного результата отнимем площадь второй комнаты.
Запишем решение.
- 44 — 24 = 20 (м2) – площадь второй и третьей комнаты
- 20 — 8 = 12 (м2)
Ответ: площадь третьей комнаты – 12 м2.
Способ 2.
Сначала узнаем, чему равна площадь первой и второй комнаты, а затем от общей площади вычтем полученный результат.
Запишем решение.
- 24 + 8 = 32 (м2) – площадь первой и второй комнат
- 44 — 32 = 12 (м2)
Ответ: площадь третьей комнаты – 12 м2.
На сегодняшнем уроке вы познакомитесь с другой единицей измерения площади — квадратными метрами, научитесь переводить квадратные метры в квадратные дециметры и сравнивать значения, а также решать задачи.
Список литературы
М.И.Моро, М.А.Бантова и другие. Математика: Учебник. 3 класс: Во 2-й, 1-й частях. -М.: «Просвещение», 2012.
М.И.Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: Часть 2, Ч. 2. -М.: «Просвещение», 2012.
М.И.Моро Уроки математики: методические рекомендации для учителей. 3 класс. -М.: Просвещение, 2012.
Нормативные документы. Мониторинг и оценка результатов обучения. -М.: «Просвещение», 2011.
«Русская школа»: программа для начальной школы. -М.: «Просвещение», 2011.
С.И.Волкова. Математика: Контрольные работы. 3 класс. -М.: Просвещение, 2012.
В.Н.Рудницкая. Тест. -М.: «Экзамен», 2012.
Дополнительные рекомендуемые ссылки на интернет-ресурсы
Интернет-портал»nsportal.ru «(Источник)
Домашнее задание
1. Найдите площадь комнаты, длина которой составляет 8 м, а ширина — 5 м.
2. Введите число.
6 м2 = … дм2
4 м2 = … дм2
9 м2 = … дм2
2 м2 = … дм2
7 м2 = … дм2
3. Сравните
1 м2 …1 дм2
1 дм2 …1 см2
8 м2 … 800 дм2
6 м2 … 700 дм2
4. Составьте задания по теме урока для своих товарищей.
Оцените урок:




