Нахождение площади прямоугольника с помощью мерок

Сегодня мы продолжим изучение площади фигур и сосредоточимся на вычислении площади прямоугольника. Мы уже знакомы с понятием площади и одной из единиц измерения – квадратным сантиметром. На уроке мы выведем правило, как вычислить площадь прямоугольника.

Мы уже умеем находить площадь фигур, которые разделены на квадратные сантиметры. Например, если у нас есть две фигуры, одна из которых имеет площадь 8 см², а другая – 7 см², мы можем легко определить их площади.

Практическая работа по нахождению площади прямоугольника

Как найти площадь прямоугольника, длины сторон которого составляют 3 см и 4 см?

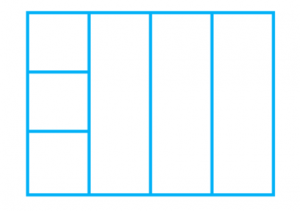
Для решения этой задачи разобьём прямоугольник на 4 полоски по 3 см² каждая. Таким образом, площадь прямоугольника будет равна:

3×4=12 см2.3×4=12 см2.

Этот же прямоугольник можно разбить на 3 полоски по 4 см².

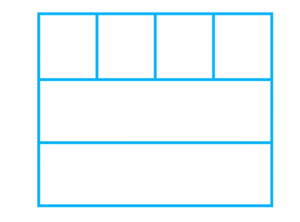
Тогда площадь будет равна:

4×3=12 см2.4×3=12 см2.

Вывод правила нахождения площади прямоугольника

В обоих случаях для нахождения площади прямоугольника мы перемножаем длины его сторон.

Теперь давайте найдем площадь каждого из примеров.

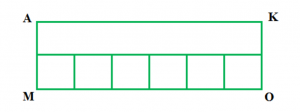
Рассмотрим прямоугольник АКМО. В одной полоске площадь составляет 6 см², а таких полосок в этом прямоугольнике 2. Следовательно, мы можем выполнить следующее действие:

6×2=12 см2.6×2=12 см2.

Здесь число 6 обозначает длину, а 2 – ширину прямоугольника. Таким образом, мы перемножили стороны, чтобы найти площадь.

Теперь рассмотрим прямоугольник KDCO. В этом прямоугольнике площадь одной полоски составляет 2 см², а таких полосок 3. Следовательно, мы можем выполнить действие:

2×3=6 см2.2×3=6 см2.

Здесь 3 см – это длина, а 2 см – ширина. Мы перемножили их и узнали площадь.

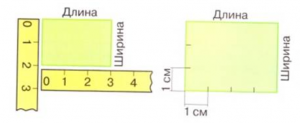
Правило нахождения площади прямоугольника

Можно сделать вывод: чтобы найти площадь прямоугольника, не обязательно разбивать его на квадратные сантиметры.

Чтобы вычислить площадь прямоугольника, нужно найти его длину и ширину (длину и ширину следует выражать в одних и тех же единицах измерения), а затем вычислить произведение полученных чисел. Площадь будет выражена в соответствующих единицах площади.

Обобщим: площадь прямоугольника равна произведению его длины и ширины.

Решение задач на нахождение площади прямоугольника и треугольника

Теперь давайте решим несколько задач.

Задача 1: Вычислите площадь прямоугольника, если его длина составляет 9 см, а ширина – 2 см.

В этой задаче известны и длина, и ширина прямоугольника. Следовательно, действуем по правилу: площадь прямоугольника равна произведению его длины и ширины.

Запишем решение:

9×2=18 см2.9×2=18 см2.

Ответ: Площадь прямоугольника составляет 18 см².

Как вы думаете, какие еще могут быть длины сторон прямоугольника с такой площадью? Поскольку площадь – это произведение длин сторон, вспомним таблицу умножения. При умножении каких чисел получается 18? Правильно, при умножении 6 и 3 тоже получится 18. Значит, у прямоугольника могут быть стороны 6 см и 3 см, и его площадь также будет равна 18 см².

Задача 2: Длина прямоугольника 8 см, а ширина 2 см. Найдите его площадь и периметр.

Зная длину и ширину прямоугольника, мы можем найти площадь, перемножив их:

8×2=16 см2.8×2=16 см2.

Для нахождения периметра необходимо сложить длину и ширину, а затем умножить на два:

$(8+2)\times 2=20\text{ см}.$

Ответ: Площадь прямоугольника 16 см², а периметр 20 см.

Задача 3: Длина прямоугольника 4 см, а ширина – 3 см. Чему равна площадь треугольника, образованного диагональю?

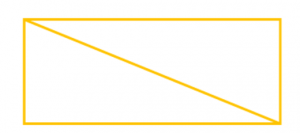
Сначала найдем площадь прямоугольника:

4×3=12 см2.4×3=12 см2.

Посмотрите на чертёж. Вы заметили, что диагональ делит прямоугольник на два равных треугольника? Следовательно, площадь одного треугольника будет в 2 раза меньше площади прямоугольника. Значит, нужно 12 уменьшить в 2 раза:

12:2=6 см2.12:2=6 см2.

Ответ: Площадь треугольника составляет 6 см².

Итоги урока

Сегодня мы познакомились с правилом вычисления площади прямоугольника и научились применять это правило при решении задач.

Список рекомендованной литературы

1. М. И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М., «Просвещение», 2012.
2. М. И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М., «Просвещение», 2012.
3. М. И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М., «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
6. С. И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В. Н. Рудницкая. Тесты. – М., «Экзамен», 2012 (127 с.).

Рекомендованные ссылки на ресурсы интернет

Социальная сеть работников образования «nsportal.ru» (Источник).

Рекомендованное домашнее задание

1. Длина прямоугольника 7 см, ширина 4 см. Найдите площадь прямоугольника.
2. Сторона квадрата 5 см. Найдите площадь квадрата.
3. Начертите возможные варианты прямоугольников, площадь которых составляет 18 см².
4. Составьте задание по теме урока для своих товарищей.