Признаки делимости на 9 и на 3
На сегодняшнем уроке мы познакомимся с признаком делимости «по сумме цифр» и научимся его применять. Также вспомним признак делимости «по последней цифре» и разберемся, как использовать оба эти признака одновременно, а также когда это возможно, а когда нет.
Если у вас возникнут трудности с пониманием темы, рекомендуем ознакомиться с уроком «Число как объект изучения (Теория чисел)».
Введение
Признаки позволяют нам быстро оценить свойства объектов.
Существует пословица: «Дыма без огня не бывает», что подразумевает, что дым является признаком огня. Однако этот признак может быть обманчивым: что-то может тлеть и дымить без наличия настоящего огня.
В математике же признаки работают всегда. К таким признакам относятся признаки делимости.
Мы уже изучили признаки делимости на 2, 5 и 10, которые основаны на последней цифре. Если последняя цифра числа делится на 2, 5 или 10, то и всё число делится на соответствующее число.
Например, число 756 делится на 2, но не делится на 5 и 10.
Сегодня мы сосредоточимся на делимости на 3 и 9.
Признак делимости на 3 и на 9
Числа 18 и 81 делятся на 9, как и 27 и 72. Аналогично, 45 и 54 делятся на 3.
Важно отметить, что порядок цифр не влияет на делимость. Вы можете проверить: если числа делятся на 3 или 9, то перестановка их цифр не изменит этого свойства.
Признак делимости на 3 и 9 формулируется следующим образом: если сумма цифр числа делится на 3 или на 9, то и само число также делится на 3 или на 9.
Это связано с тем, что перестановка цифр не изменяет их сумму.
Как применять признак делимости на 3
Как увидеть, что число 72 делится на 3?
Например, так:
72 = 60 + 12. 60 делится на 3 и 12 делится на 3, значит, и все число делится на 3.
Это правило очень полезное, и мы его часто используем.
Если в сумме оба слагаемых делятся на некое число, то вся сумма делится на это число.
A = B + C
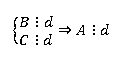
Если одно делится, а другое нет, то и вся сумма не делится.
A = B + C
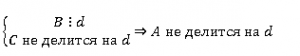
Вернемся к числу 72.
Разложение на 60 и 12 удобно, но не дает нам общего правила, алгоритма, как действовать с другими числами.
Вспомним, что обозначает десятичная запись числа.
![]()
Первое слагаемое (7 * 9) делится на 3.
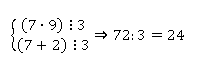
(7 + 2) тоже делится на 3. Но это и есть сумма цифр. Если бы она не делилась, то и все число не делилось бы.
Например, разделим число 73 на 3.
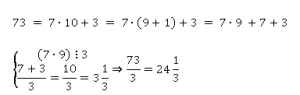
И этот алгоритм можно применить к любому числу.
Задача 1
Возьмем число побольше, 2382, и попробуем понять, делится ли оно на 3 и на 9.
Шаг первый
Вспомним, что означает десятичная запись числа, и запишем число в эквивалентной форме:
![]()
Распишем каждое разрядное число:
![]()
Раскроем скобки:
![]()
Сгруппируем слагаемые:
![]()
Получили две суммы.
Шаг второй
Используем свойство делимости суммы: если оба слагаемых делятся, то сумма делится, если одно делится, другое нет, то сумма не делится.
У нас в первых скобках каждое слагаемое делится на 3 и на 9, значит, и вся сумма делится на 3 и на 9.
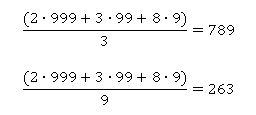
Таким образом, делимость всего нашего числа зависит теперь от последней суммы. Если она делится на 3 или 9, то и все число делится, если нет, то и все число нет.
Но во вторых скобках и есть сумма цифр исходного числа.
То есть число делится на 3 или на 9 тогда и только тогда, когда сумма его цифр делится на 3 или на 9.
Проверим делимость в нашем случае:
2 + 3 + 8 + 2 = 15 делится на 3, но не делится на 9.

Ответ: 2382 делится на 3, но не делится на 9.
Есть удобный инструмент – теория сравнений.
С помощью него объяснение признака делимости на 3 и на 9 очень короткое. О нем рассказывается в конце урока.
Теория сравнений
С помощью теории сравнений можно кратко объяснить признак делимости на 3 и 9. Мы выбираем число, например 3, и называем его модулем. Два числа считаются одинаковыми, если они дают одинаковый остаток при делении на 3.
Например, числа 6 и 9 дают одинаковый остаток при делении на 3, следовательно, они сравнимы по модулю 3.
Применение нескольких признаков делимости
Рассмотрим, как использовать сразу два признака: по последней цифре и по сумме цифр.
Пример: Делится ли число 12 348 на 6?
- Делится на 2 (последняя цифра 8 делится на 2).
- Делится на 3 (сумма цифр 1 + 2 + 3 + 4 + 8 = 18 делится на 3).
- Значит, 12 348 делится на 6.
Пример: Делится ли число 4525 на 15?
- Делится на 5 (последняя цифра 5).
- Не делится на 3 (сумма 4 + 5 + 2 + 5 = 16 не делится на 3).
- Следовательно, 4525 не делится на 15.
Вопросы
Ответьте на следующие вопросы:
- Если мы знаем, что число делится на 9, нужно ли проверять, делится ли оно на 3?
- Если мы знаем, что число делится на 3, что можно сказать о его делимости на 9?
Теория сравнений и признак делимости на 3 и 9
Выбираем число, например 3. Будем называть его модулем.
Два числа считаем одинаковыми, если они дают одинаковый остаток при делении на 3.
Например, ![]()
Такие числа будем называть сравнимыми по модулю 3.
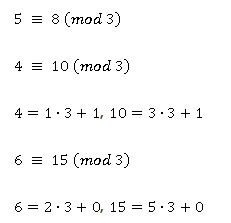
Очевидно, все разрядные числа сравнимы с единицей по модулям 3 и 9.
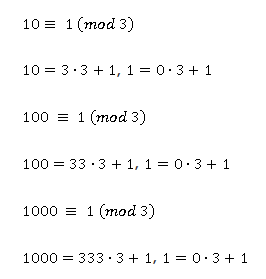
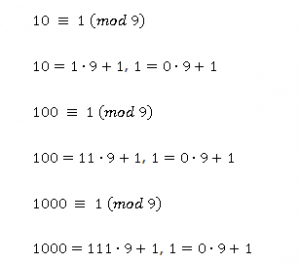
Доказательство признака делимости на 3 и на 9
Рассмотрим число.
![]()
Все разрядные числа можно заменить на единицы, если сравнивать по модулям 3 и 9.
![]()
То есть любое число и число, полученное как сумма его цифр, сравнимы по модулям 3 и 9. Значит, они делятся или не делятся на них одновременно.
Список литературы
- Виленкин Н. Я., Жохов В. И., Чесноков А. С. и др. «Математика 6». М.: Мнемозина, 2012.
- Мерзляк А. Г., Полонский В. В., Якир М. С. «Математика 6 класс». Гимназия, 2006.
- Депман И. Я., Виленкин Н. Я. «За страницами учебника математики». Просвещение, 1989.
Дополнительные ресурсы
- Интернет-портал «school-assistant.ru»
- Интернет-портал «math-prosto.ru»
Домашнее задание
Виленкин Н. Я., Жохов В. И., Чесноков А. С. и др. «Математика 6». М.: Мнемозина, 2012. Выполните задания № 64, 86, 92.
Оцените урок:




