Сложение чисел с разными знаками

На уроках математики в 6 классе мы уже освоили сложение чисел и понимаем, что знаки «плюс» и «минус» обозначают разные величины. Теперь пришло время перейти на новый уровень и изучить, как правильно складывать числа с различными знаками.

Сложение чисел с разными знаками представляет собой процесс, при котором из большего по модулю числа вычитается меньшее. Затем к полученному результату добавляется знак числа с большим модулем. Например, для чисел -7 и 3 вычисление будет следующим:

|7| — |3| = 4
Знак результата будет «-» (так как -7 имеет больший модуль)
Итог: -4

Основные определения
Целые числа — это набор чисел, включающий натуральные числа, отрицательные целые числа и ноль.

Отрицательные целые числа — это целые числа со знаком «минус», которые всегда меньше нуля. Примеры: -1, -945, -20.

Положительные целые числа — это целые числа со знаком «плюс», которые всегда больше нуля. Примеры: 11, 500, 1387.

Каждое положительное число имеет свое противоположное число, которое отличается лишь знаком. Такие числа называются противоположными.

Противоположные числа не равны, но имеют одинаковый модуль. Модуль положительного числа равен самому числу, а у отрицательного — его противоположному, то есть положительному. Например:

∣8∣ = 8, ∣-8∣ = 8.

Действительные числа — это числа, которые могут быть представлены в виде конечной или бесконечной десятичной дроби.

Рациональные числа — это числа, которые можно выразить в виде положительной или отрицательной обыкновенной дроби или нуля.

Правило сложения чисел с разными знаками
Положительное число можно воспринимать как доход, а отрицательное — как расходы или долг. Чтобы понять, сколько мы заработали или потратили, необходимо сравнить модули этих чисел.

Например, если родители дали нам триста рублей на карманные расходы, и в конце недели у нас осталось немного денег, это означает, что расходы были меньше доходов. Если же нам пришлось попросить еще 50 рублей, значит, расходы превысили доход. Если расходы равны доходам, то у нас будет нулевой остаток.

Теперь сформулируем правило сложения чисел с разными знаками:

1. Найдите модули слагаемых.
2. Сравните полученные значения.
   • Если модули равны, исходные числа противоположны (близнецы) — их сумма равна нулю.
   • Если модули не равны, запомните знак числа с большим модулем.
3. Из большего модуля вычтите меньший.
4. Перед полученным числом поставьте знак того слагаемого, модуль которого больше.

Это правило сводит сложение чисел с разными знаками к вычитанию меньшего числа из большего. В результате сложения положительного и отрицательного числа может получиться положительное, отрицательное число или ноль.

Рассмотрим это на примере: 2 + (-6) = -4.

• Знаки слагаемых: разные
• Знак суммы: «−»
• Модули слагаемых: ∣2∣ = 2, ∣-6∣ = 6
• Модуль суммы: ∣-4∣ = 4
• Разность модулей: ∣-6∣ — ∣2∣ = 4 (6 — 2 = 4)
• Знак результата (-4) совпадает со знаком числа с большим модулем (-6).

Повторим основные шаги: чтобы сложить числа с разными знаками, нужно:

• Из большего модуля вычесть меньший.
• Поставить знак слагаемого с большим модулем перед полученным результатом.

Этот алгоритм сложения чисел с различными знаками применим для целых, рациональных и действительных чисел.

Примеры сложения чисел с разными знаками

Сложение чисел с разными знаками требует внимательности и последовательности. Давайте рассмотрим пример, следуя вышеописанному правилу.

Пример 1. Сложим числа -8 и 1.

Для начала выполним все шаги, необходимые для сложения положительного и отрицательного числа.

1. Найдем модули слагаемых: для -8 модуль равен 8, а для 1 — 1.
2. Сравнив модули, мы видим, что модуль числа -8 больше, чем модуль числа 1. Запоминаем знак минус.
3. Теперь вычтем меньший модуль из большего: 8 — 1 = 7.

После этого добавим знак, соответствующий большему модулю, и получаем: -7.

Таким образом, сложение чисел с разными знаками завершено. Ответ: (-8) + 1 = -7.

Пример 2.

Сложить положительное число и отрицательное число -1,25.

Чтобы сложить рациональные числа с разными знаками, которые не являются целыми, их следует представить в виде обыкновенных или десятичных дробей.

Как решаем:

 
Представим числа в виде обыкновенных дробей.
Для этого выполним переход от смешанного числа к неправильной дроби:

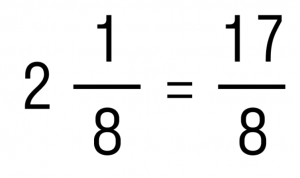
, и переводим десятичную дробь в обыкновенную:

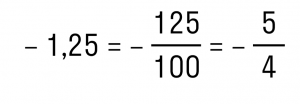
Теперь можно воспользоваться правилом сложения чисел с разными знаками.
Модули складываемых чисел равны 17/8 и 5/4. Чтобы нам было удобнее считать, приведем дроби к общему знаменателю — получаем 17/8 и 10/8.

Сравним обыкновенные дробей 17/8 и 10/8.
Так как 17>10, то .

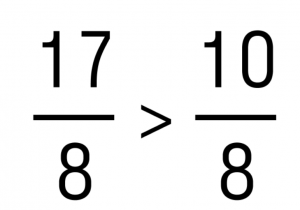
Это значит, что слагаемое со знаком плюс имеет больший модуль, поэтому запоминаем знак плюс.

Теперь из большего модуля вычитаем меньший, то есть, выполним вычитание дробей с одинаковыми знаменателями:

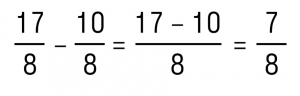
Осталось перед полученным числом поставить знак плюс, получаем:
, то есть 7/8.
На этом сложение чисел с разными знаками завершено. Краткая запись решения выглядит так:

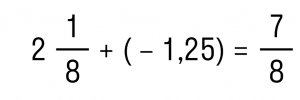
Пример 3. Чему равна сумма чисел

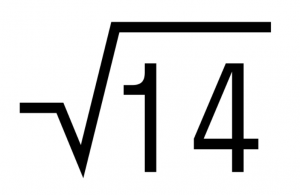
и

?

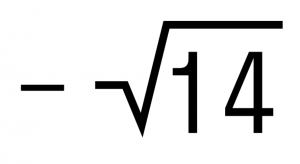
Как решаем:

Замечаем, что у складываемых чисел разные знаки, а их модули равны. Значит эти числа являются противоположными, а сумма противоположных чисел равна нулю.

Получается вот так:

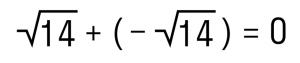
Ответ: 0.

Важно помнить, что при сложении действительных чисел с разными знаками результат можно записывать не в виде бесконечной десятичной дроби, а в виде числового выражения, которое содержит корни, степени, логарифмы и прочее.

Например, результат сложения двух чисел с разными знаками -1 и π записывается так: π — 1.